Question

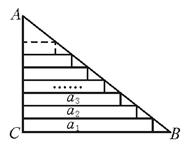
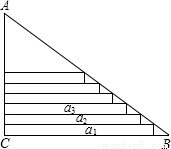
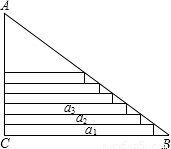
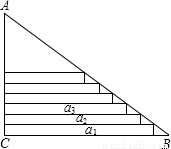
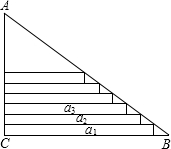某班在布置新年联欢会会场时，需要将直角三角形彩纸裁成长度不等的矩形彩条．如图，在Rt△ABC中，∠C=90°，AC=30cm，AB=50cm，依次裁下宽为1cm的矩形纸条a₁，a₂，…，a_n．若使裁得的矩形纸条的长不小于5cm，则每张直角三角形彩纸能裁成的矩形纸条的总数为（　　）

• A、24
• B、25
• C、26
• D、27

Answer 1

分析：把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求解即可．

解答：解：设所求的矩形有x张，其中最小的矩形的长为ycm，
则

y

40

=

30-1•x

30

∴y=40-

4

3

x，
又∵y≥5，
∴40-

4

3

x≥5，
∴x≤26

1

4

，
∴最多能裁26张．
故选C．

点评：本题主要是体现了方程的思想，有一定难度．