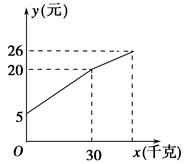
题目内容
如图，直线x=2与反比例函数y＝
和y＝?
的图象分别交于A、B两点，若点P是y轴上任意一点，则△PAB的面积是( )．
和y＝?的图象分别交于A、B两点，若点P是y轴上任意一点，则△PAB的面积是( )．
先分别求出A、B两点的坐标，得到AB的长度，再根据三角形的面积公式即可得出△PAB的面积．
解：∵把x=2分别代入y＝、y＝?，得y=1、y=-
．
∴A（2，1），B（2，-），
∴AB=1-（-）=．
∵P为y轴上的任意一点，
∴点P到直线x=2的距离为2，
∴△PAB的面积=AB×2=AB=．
故答案是：
解：∵把x=2分别代入y＝
、y＝?，得y=1、y=-．∴A（2，1），B（2，-
），∴AB=1-（-
）=．∵P为y轴上的任意一点，
∴点P到直线x=2的距离为2，
∴△PAB的面积=
AB×2=AB=．故答案是：
练习册系列答案
相关题目
与x轴、y轴分别交于点A、B，点C在线段AB上，且
．
上时，求该抛物线的表达式；
（
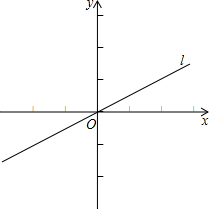
为正整数）与两坐标轴围成的三角形面积为
，则
.
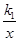(k1＞0)与一次函数y2＝k2x＋1(k2≠0)相交于A、B两点，AC⊥x轴于点C.若△OAC的面积为1，且tan∠AOC＝2.
