题目内容
【题目】在平面直角坐标系中,边长为![]() 的正方形
的正方形![]() 的两顶点
的两顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,
点顺时针旋转, ![]() 与
与![]() 轴相交于点
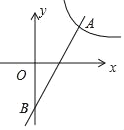
轴相交于点![]() ,如图,当
,如图,当![]() 时,点
时,点![]() 的坐标为( )
的坐标为( )
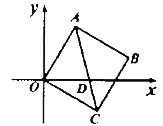
A. 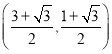 B.
B. 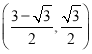 C.
C. 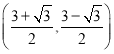 D.
D. 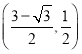
【答案】C
【解析】
过点A作AE⊥x轴,作BF⊥AE,垂足分别是E,F,可证△AFB≌△AEO,所以AF=OE,BF=AE,根据OA=![]() ,根据含有30°的直角三角形性质可求OE,AE的长度,即可求B点坐标.
,根据含有30°的直角三角形性质可求OE,AE的长度,即可求B点坐标.
过点A作AE⊥x轴,作BF⊥AE,垂足分别是E,F.如图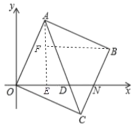
∵∠AOD=60°,AE⊥OD
∴∠OAE=30°
∴OE=![]() OA=
OA=![]() ,AE=
,AE=![]() OE=
OE=![]()
∵∠OAE+∠AOE=90°,∠OAE+∠EAB=90°
∴∠AOE=∠AFB,且∠AEO=∠AFB=90°,OA=OB
∴△AOE≌△AFB(AAS)
∴AF=OE=![]() ,BF=AE=
,BF=AE=![]()
∴EF=![]() -
-![]()
∴B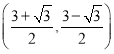
故选:C.

【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?