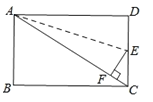
题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中线,作
的中线,作![]() 于
于![]() ,点
,点![]() 在
在![]() 延长线上,
延长线上,![]() ,连接
,连接![]() 、
、![]() .
.
![]() 求证:四边形
求证:四边形![]() 为菱形;
为菱形;
![]() 把
把![]() 分割成三个全等的三角形,需要两条分割线段,若
分割成三个全等的三角形,需要两条分割线段,若![]() ,求两条分割线段长度的和.
,求两条分割线段长度的和.

【答案】![]() 证明见解析;(2)两条分割线段长度的和为
证明见解析;(2)两条分割线段长度的和为![]() .
.
【解析】
(1)容易证三角形BCD为等边三角形,又DE=AD=BD,再证三角形DBE为等边三角形四边相等的四边形BCDE为菱形.
(2)画出图形,证出BM+MN=AM+MC=AC=6即可.
(1)∵∠ACB=90°,∠A=30°,CD为△ABC的中线,∴BC=![]() AB,CD=
AB,CD=![]() AB=AD,∴∠ACD=∠A=30°,∴∠BDC=30°+30°=60°,∴△BCD是等边三角形.
AB=AD,∴∠ACD=∠A=30°,∴∠BDC=30°+30°=60°,∴△BCD是等边三角形.
∵CO⊥AB,∴OD=OB,∴DE=BE.
∵DE=AD,∴CD=BC=DE=BE,∴四边形BCDE为菱形;
(2)作∠ABC的平分线交AC于N,再作MN⊥AB于N,如图所示:
则MN=MC=![]() BM,∠ABM=∠A=30°,∴AM=BM.
BM,∠ABM=∠A=30°,∴AM=BM.
∵AC=6,∴BM+MN=AM+MC=AC=6;
即两条分割线段长度的和为6.

练习册系列答案
相关题目