题目内容
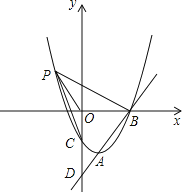
【题目】如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.

(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
【答案】(1)16;(2)当x=2时,DM有最大值为1.
【解析】
(1)由已知∠AEB=∠BFC=90°,AB=BC,结合∠ABE=∠BCF,证明△ABE≌△BCF,可得AE=BF,于是AE2+CF2=BF2+CF2=BC2=16为常数.
(2)设AP=x,则PD=4﹣x,由已知∠DPM=∠PAE=∠ABP,△PDM∽△BAP,列出关于x的二次函数,求出DM的最大值.
解:(1)由已知∠AEB=∠BFC=90°,AB=BC,
又∵∠ABE+∠FBC=∠BCF+∠FBC,∴∠ABE=∠BCF.
∵在△ABE和△BCF中,AB=BC,∠ABE=∠BCF,∠AEB=∠BFC,
∴△ABE≌△BCF(AAS).
∴AE=BF.∴AE2+CF2=BF2+CF2=BC2=16为常数.
(2)设AP=x,则PD=4﹣x,
由已知∠DPM=∠PAE=∠ABP,∴△PDM∽△BAP.
∴![]() ,即
,即![]() .
.
∴![]() .
.
∵![]() <0,当x=2时,DM有最大值为1.
<0,当x=2时,DM有最大值为1.

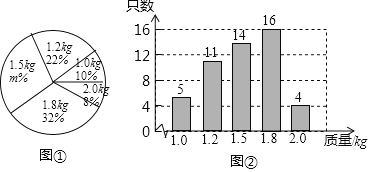
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
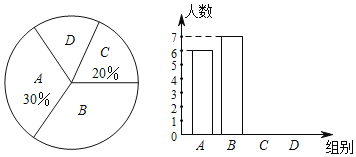
【题目】某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数/人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |
频数分布表
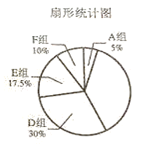
请根据图表中的信息解答下列问题:
(1)求频数分布表中m的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。
【题目】我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
代号 | 活动类型 |
A | 经典诵读与写作 |
B | 数学兴趣与培优 |
C | 英语阅读与写作 |
D | 艺体类 |
E | 其他 |
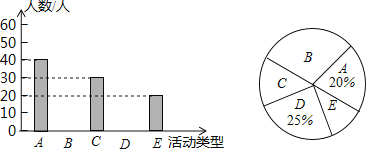
为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).
(1)此次共调查了 名学生.
(2)将条形统计图补充完整.
(3)“数学兴趣与培优”所在扇形的圆心角的度数为 .
(4)若该校共有2000名学生,请估计该校喜欢A、B、C三类活动的学生共有多少人?
(5)学校将从喜欢“A”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.