题目内容
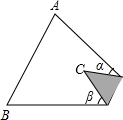
如图，Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，若将AC沿AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．
∵△ABC是直角三角形，AC=6cm，BC=8cm，
∴AB=
=
=10（cm），
∵△AED是△ACD翻折而成，
∴AE=AC=6cm，∠AED=90°，
设DE=CD=xcm，
∴BE=AB-AE=10-6=4（cm），
在Rt△BDE中，BD2=DE2+BE2，
即（8-x）2=42+x2，
解得：x=3．
故CD的长为3cm．
∴AB=
| AC2+BC2 |
| 62+82 |
∵△AED是△ACD翻折而成，
∴AE=AC=6cm，∠AED=90°，
设DE=CD=xcm，
∴BE=AB-AE=10-6=4（cm），
在Rt△BDE中，BD2=DE2+BE2，
即（8-x）2=42+x2，
解得：x=3．
故CD的长为3cm．
练习册系列答案
全优点练单元计划系列答案
相关题目
