题目内容
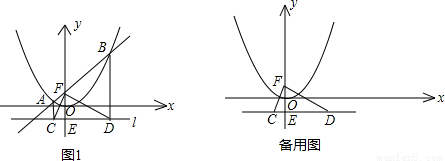
已知,如图1,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,抛物线
,抛物线![]() 上的两点
上的两点![]() 的横坐标分别为
的横坐标分别为![]() 1和4,直线
1和4,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求证:![]() ;
;
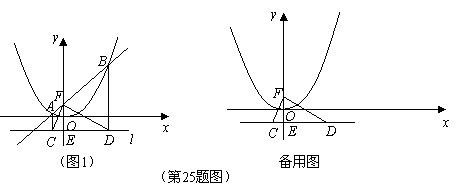 (3)点
(3)点![]() 是抛物线
是抛物线![]() 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,是否存在点
,是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
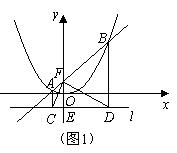
(1)解:方法一,如图1,当![]() 时,
时,![]()
当![]() 时,
时,![]()
 ∴
∴![]()
![]()
设直线![]() 的解析式为
的解析式为![]()
则 解得
解得![]()
∴直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
![]()
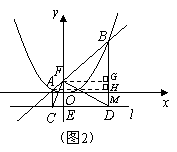
方法二:求![]() 两点坐标同方法一,如图2,作
两点坐标同方法一,如图2,作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,则四边形
,则四边形![]() 和四边形
和四边形![]() 均为矩形,设
均为矩形,设![]()
![]()
![]()
![]()
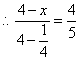 解得
解得![]()
![]()
(2)证明:方法一:在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
由(1)得![]()
![]()
![]()
![]()
![]()
![]()
![]()
方法二:由 (1)知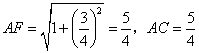
![]()
同理:![]()
![]()
![]()
![]()
![]()
同理:![]()
![]()
即![]()
(3)存在.
解:如图3,作![]() 轴,垂足为点
轴,垂足为点![]() ··· 9分
··· 9分
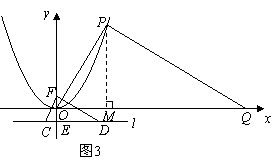 又
又![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
①当![]() 时,
时,
![]()
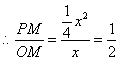
解得![]()
![]()
②当![]() 时,
时,
![]()
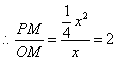
解得![]()
![]()
综上,存在点![]() 、
、![]() 使得
使得![]() 与
与![]() 相似.
相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
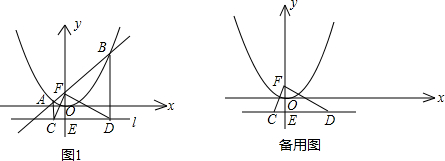
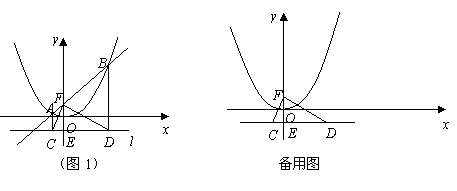

 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.