题目内容
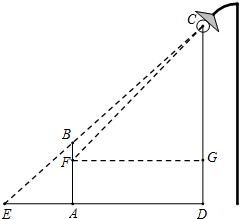
如图,水平地面上A处站着身高为1.8m的人(可以看成线段AB),他的正前方往上有一盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).(1)在路灯照射下这个人与地面形成的影子可以看成是线段AE,求AE的长度;
(2)又已知这个人的眼睛(可以看成点F)离开地面的高度AF=1.7m,他站在A处观看路灯时的仰角为∠CFG(图中FG⊥CD),求∠CFG的度数.(精确到1°)

【答案】分析:(1)根据CD⊥AD,AD⊥AB可得出 =
=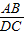 ,然后代入AB及CD的长度即可得出AE的长度.
,然后代入AB及CD的长度即可得出AE的长度.
(2)根据FG⊥CD可判断出四边形ADGF是矩形,然后可确定CG的长度,继而可求出tan∠CFG的值,也就得出了答案.
解答:解:(1)∵CD⊥AD,AD⊥AB,
∴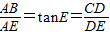 ,
,
即 ,
,
AE+6.4=5AE,
解得AE=1.6(m);
(2)∵FG⊥CD,
∴四边形ADGF是矩形,
∴FG=AD=6.4,DG=AF=1.7,
∴CG=7.3,
∴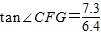 ,
,
∴∠CFG≈49°.
点评:此题主要考查解直角三角形的应用,关键是要求学生能借助仰角构造直角三角形并解直角三角形.
 =
=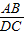 ,然后代入AB及CD的长度即可得出AE的长度.
,然后代入AB及CD的长度即可得出AE的长度.(2)根据FG⊥CD可判断出四边形ADGF是矩形,然后可确定CG的长度,继而可求出tan∠CFG的值,也就得出了答案.
解答:解:(1)∵CD⊥AD,AD⊥AB,
∴
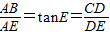 ,
,即
 ,
,AE+6.4=5AE,
解得AE=1.6(m);
(2)∵FG⊥CD,
∴四边形ADGF是矩形,
∴FG=AD=6.4,DG=AF=1.7,
∴CG=7.3,
∴
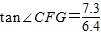 ,
,∴∠CFG≈49°.
点评:此题主要考查解直角三角形的应用,关键是要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
 盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).
盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB). (2013•大连一模)如图,为了测量某建筑物CD的高度,测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°,然后在水平地面上向建筑物前进42米,此时自B处测得建筑物顶部C的仰角是60°.已知测角仪的高度始终是1.5米,则该建筑物CD的高度约为
(2013•大连一模)如图,为了测量某建筑物CD的高度,测量人员先在地面上用测角仪AE自A处测得建筑物顶部C的仰角是30°,然后在水平地面上向建筑物前进42米,此时自B处测得建筑物顶部C的仰角是60°.已知测角仪的高度始终是1.5米,则该建筑物CD的高度约为 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).以AB所在直线为x轴,OM所在直线为y轴建立平面直角坐标系. 盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).
盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).