Question

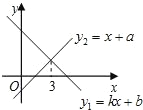
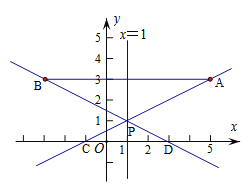
【题目】如图，在平面直角坐标系中，已知点A（5，3），点B（－3，3），过点A的直线（m为常数）与直线x＝1交于点P，与x轴交于点C，直线BP与x轴交于点D。

（1）求点P的坐标；

（2）求直线BP的解析式，并直接写出△PCD与△PAB的面积比；

（3）若反比例函数（k为常数且k≠0）的图象与线段BD有公共点时，请直接写出k的最大值或最小值。

Answer 1

【答案】（1）P（1，1）； （2） ；（3）当k＜0时，最小值为－9；当k＞0时，最大值为

【解析】试题分析：把点坐标代入一次函数，求得的值，进而求得点的坐标.

用待定系数法即可求得直线的解析式,直接计算面积即可求出它们的比值.

分成和两种情况进行讨论.

试题解析：（1）∵过点A（5，3），

解得：

∴y=，

当时，∴，

∴

（2）设直线BP的解析式为y=ax＋b，

根据题意，得

解得：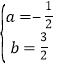

∴直线BP的解析式为，

点

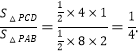
（3）当时，经过点时，有最小值为－9；

当时，联立方程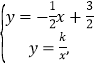 整理得，

解得：

即最大值为.