题目内容
我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
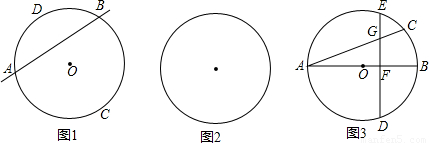
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
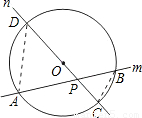
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
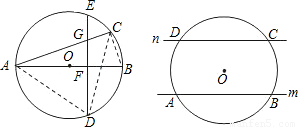
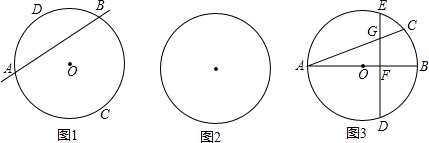
(3)如图3,其中AB是圆O的直径,AC是弦,D是
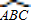 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
【答案】分析:(1)本题AB⊥DE,满足垂径定理,可以写出垂径定理的结论;
(2)根据三角形相似就可以证出;
(3)若点C和点E重合,设∠BAC=x,又D是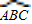 的中点,根据2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度数.
的中点,根据2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度数.
解答:解:(1)弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等.
(写对一个给(1分),写对两个给2分)
(2)如图,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
结论:PA•PB=PC•PD.
证明:连接AD,BC,
∵∠APD=∠BPC,∠D=∠B
∴△APD∽△BPC
∴PA•PB=PC•PD;
(3)若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称,(8分)
设∠BAC=x,则∠BAD=x,∠ABC=90°-x,(9分)
又D是 的中点,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC,
的中点,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC,
即2•2x=180°-(90°-x),(10分)
解得x=∠BAC=30°.(11分)
(若求得AB=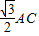 或AF=3•FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)
或AF=3•FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)
点评:本题主要考查了垂径定理以及相交弦定理的证明过程,正确理解题意,读懂图意是解决本题的关键.
(2)根据三角形相似就可以证出;
(3)若点C和点E重合,设∠BAC=x,又D是
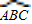 的中点,根据2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度数.
的中点,根据2∠CAD=∠CAD+ACD=180°-∠ABC,就可以求出∠BAC的度数.解答:解:(1)弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等.
(写对一个给(1分),写对两个给2分)

(2)如图,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
结论:PA•PB=PC•PD.
证明:连接AD,BC,
∵∠APD=∠BPC,∠D=∠B
∴△APD∽△BPC
∴PA•PB=PC•PD;

(3)若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称,(8分)
设∠BAC=x,则∠BAD=x,∠ABC=90°-x,(9分)
又D是
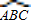 的中点,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC,
的中点,所以2∠CAD=∠CAD+∠ACD=180°-∠ABC,即2•2x=180°-(90°-x),(10分)
解得x=∠BAC=30°.(11分)
(若求得AB=
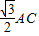 或AF=3•FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)
或AF=3•FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)点评:本题主要考查了垂径定理以及相交弦定理的证明过程,正确理解题意,读懂图意是解决本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

 ⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
⊥AB于点F.请找出点C和点E重合的条件,并说明理由. 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.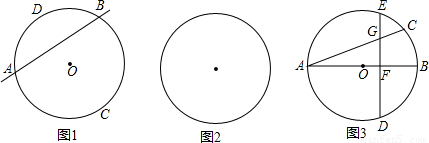
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.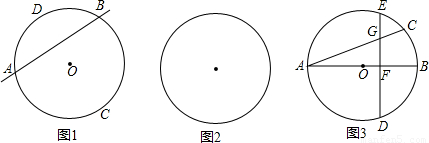
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.