题目内容
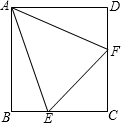
已知△ABC中,∠ACB=135°,将△ABC绕点A顺时针旋转90°,得到△AED,连接CD,CE.
(1)求证:△ACD为等腰直角三角形;
(2)若BC=1,AC=2,求四边形ACED的面积.

(1)求证:△ACD为等腰直角三角形;
(2)若BC=1,AC=2,求四边形ACED的面积.

证明:(1)∵△AED是△ABC旋转90°得到的,
∴△ABC≌△AED,
∴∠CAD=90°,AC=AD,∠ADE=∠ACB=135°,
∴△ACD是等腰直角三角形;
(2)∵△ACD是等腰直角三角形,
∴∠ADC=∠ACD=45°,AC=AD=2,
∴CD=
=2
,
由(1)知,∠ADE=135°,
∴∠CDE=∠ADE-∠ADC=90°,
∵DE=BC=1,
∴S四边形ADEC=S△ACD+S△CDE=
AC•AD+
CD•DE=
×2×2+
×2
×1=2+
.

∴△ABC≌△AED,
∴∠CAD=90°,AC=AD,∠ADE=∠ACB=135°,
∴△ACD是等腰直角三角形;
(2)∵△ACD是等腰直角三角形,
∴∠ADC=∠ACD=45°,AC=AD=2,
∴CD=
| AC2+AD2 |
| 2 |
由(1)知,∠ADE=135°,
∴∠CDE=∠ADE-∠ADC=90°,
∵DE=BC=1,
∴S四边形ADEC=S△ACD+S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |


练习册系列答案
相关题目