Question

【题目】如图，四边形ABCD和AEGF都是菱形，∠A＝60°，AD＝3，点E，F分别在AB，AD边上（不与端点重合），当△GBC为等腰三角形时，AF的长为_____．

Answer 1

【答案】3﹣或2．

【解析】

分两种情形：①如图1中，当CB=CG时，连接BD交AC于点O，②如图2中，当GC=GB时，作GM⊥BC于M，先证明 ， ，求出AG即可解决问题．

①如图1中,

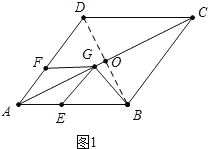
当CB=CG时，连接BD交AC于点O，

∵四边形ABCD是菱形，

∴AD=AB=3，AO=OC，

∵∠BAD=60°，

∴△ABD是等边三角形，

∴

同理

∴

∴ ，

∴ .

②如图2中,

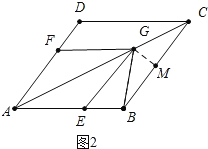
当GC=GB时，作GM⊥BC于M，

在RT△GCM中，∠GMC=90°，CM=BM= ,∠GCM=30°

∴

∴ ，

∴

∴AF=2.

故答案为：3﹣或2．