题目内容
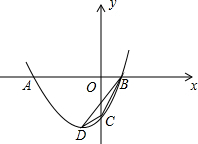 抛物线y=ax2+bx+c(a>0)经过点A(-3
抛物线y=ax2+bx+c(a>0)经过点A(-3| 3 |
| 3 |
(1)若c=ka,求系数k的值;
(2)当∠ACB=90°,求a及h的值;
(3)当∠ACB≥90°时,经过探究、猜想请你直接写出h的取值范围.
(不要求书写探究、猜想的过程)
分析:(1)由于A、B是抛物线与x轴的两个交点,可用交点式表示该抛物线的解析式,展开后即可得到c、a的关系式,进而可判断出k的值.
(2)若∠ACB=90°,根据射影定理即可求得OC的长,从而得到C点的坐标,用待定系数法即可求得抛物线的解析式,进而可求得顶点D的坐标;过D作DE⊥y轴于E,过B作BF⊥CH于F,那么BF就是所求的h,延长DC交x轴于H,易证得△DCE∽△HCO,根据得到的比例线段,可求得OH的长,从而得到BH的值,易求得∠OHC的度数,在Rt△BFH中,通过解直角三角形即可求得BF的长即h的值.
(3)∠ACB≥90°时,h随∠ACB度数的增大而减小,由此可确定h的取值范围.
(2)若∠ACB=90°,根据射影定理即可求得OC的长,从而得到C点的坐标,用待定系数法即可求得抛物线的解析式,进而可求得顶点D的坐标;过D作DE⊥y轴于E,过B作BF⊥CH于F,那么BF就是所求的h,延长DC交x轴于H,易证得△DCE∽△HCO,根据得到的比例线段,可求得OH的长,从而得到BH的值,易求得∠OHC的度数,在Rt△BFH中,通过解直角三角形即可求得BF的长即h的值.
(3)∠ACB≥90°时,h随∠ACB度数的增大而减小,由此可确定h的取值范围.
解答:解:(1)因为A(-3
,0),B(
,0)在抛物线y=ax2+bx+c(a>0)上,
所以有,y=a(x+3
)(x-
)=a(x2+2
x-9),
又因为c=-9a
所以k=-9.
(2)由于∠ACB=90°时,
∵OC⊥AB,
∴∠AOC=∠BOC=90°.
可得∠ACO=∠OBC.
∴△AOC∽△COB.
∴
=
,
即OC2=OA•OB=3
×
=9.
∴OC=3.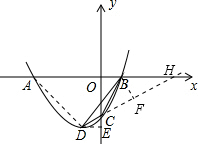
∵C(0-3),由(1)知-9a,
∴a=
.
过D作DE⊥OC交y轴于点E,延长DC交x轴于点H,过B作BF⊥CH于点F.
即BF是边DC的高h.
因为D是抛物线的顶点,
所以D(-
,-4),
故OE=4,又OC=3,可得CE=1,DE=
.
易证△HCO∽△DCE,有
=
=
=3,
故OH=3DE=3
,BH=OH-OB=2
.
由于∠COH=90°,OC=3,OH=3
,由勾股定理知CH=6,有∠OHC=30°,
又因为在Rt△BHF中,BH=2
,
所以BF=
,即h=
.
(3)当∠ACB≥90°时,猜想0<h≤
.
| 3 |
| 3 |
所以有,y=a(x+3
| 3 |
| 3 |
| 3 |
又因为c=-9a
所以k=-9.
(2)由于∠ACB=90°时,
∵OC⊥AB,
∴∠AOC=∠BOC=90°.
可得∠ACO=∠OBC.
∴△AOC∽△COB.
∴
| AO |
| OC |
| OC |
| OB |
即OC2=OA•OB=3
| 3 |
| 3 |
∴OC=3.

∵C(0-3),由(1)知-9a,
∴a=
| 1 |
| 3 |
过D作DE⊥OC交y轴于点E,延长DC交x轴于点H,过B作BF⊥CH于点F.
即BF是边DC的高h.
因为D是抛物线的顶点,
所以D(-
| 3 |
故OE=4,又OC=3,可得CE=1,DE=
| 3 |
易证△HCO∽△DCE,有
| HO |
| DE |
| CO |
| EC |
| 3 |
| 1 |
故OH=3DE=3
| 3 |
| 3 |
由于∠COH=90°,OC=3,OH=3
| 3 |
又因为在Rt△BHF中,BH=2
| 3 |
所以BF=
| 3 |
| 3 |
(3)当∠ACB≥90°时,猜想0<h≤
| 3 |
点评:此题考查了二次函数解析式的确定、相似三角形的判定和性质、勾股定理等知识的综合应用;(2)题中,能够根据已知条件正确的构造与所求相关的相似三角形,是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知点(2,8)在抛物线y=ax2上,则a的值为( )
| A、±2 | ||
B、±2
| ||
| C、2 | ||
| D、-2 |
若(2,0)、(4,0)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线( )
| A、x=0 | B、x=1 | C、x=2 | D、x=3 |


 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.