题目内容
已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:当a取不等于1的实数时,此方程总有两个实数根;
(2)若m,n(![]() )是此方程的两根,并且
)是此方程的两根,并且![]() .直线l:
.直线l:![]() 交x轴于点A,交y轴于点B.坐标原点O关于直线l的对称点
交x轴于点A,交y轴于点B.坐标原点O关于直线l的对称点![]() 在反比例函数
在反比例函数![]() 的图象上,求反比例函数
的图象上,求反比例函数![]() 的解析式;
的解析式;
(3)在(2)成立的条件下,将直线l绕点A逆时针旋转角![]() ,得到直线
,得到直线![]() ,
,![]() 交y轴于点P,过点P作x轴的平行线,与上述反比例函数
交y轴于点P,过点P作x轴的平行线,与上述反比例函数![]() 的图象交于点Q,当四边形
的图象交于点Q,当四边形![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值.
的值.
 |
(1)证明:
∵![]() 为关于x的一元二次方程,
为关于x的一元二次方程,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
∴![]() ≥
≥![]() .
.
∴当a取不等于1的实数时,此方程总有两个实数根.
(2)解:关于x的一元二次方程![]() 的两根为
的两根为
![]() .
.
∴![]() .
.
∵m,n是方程的两根,且![]() ,
,
∴ .
.
∴![]() . … ∴
. … ∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴直线l的解析式为![]() .
.
∴直线l与x轴交点![]() ,与y轴交点
,与y轴交点![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴坐标原点O关于直线l的对称点![]() 的坐标为
的坐标为![]() .
.
∴反比例函数的解析式为![]() .
.
(3)解:设点P的坐标为(0, p),延长PQ和![]() 交于点G.
交于点G.
∵![]() 轴,与反比例函数图象交于点Q,
轴,与反比例函数图象交于点Q,
∴四边形AOPG为矩形.
∴Q的坐标为![]() .
.
∴![]() .
.
当![]() ,即
,即![]() 时,
时,
∵![]() ,
,
 ∴
∴![]()
![]()
![]()
![]() .
.
∴![]() .
.
∴![]() .
.
经检验,![]() 符合题意.
符合题意.
∴![]() .
.
∴![]() .
.
点A关于y轴的对称点为![]() ,连结
,连结![]() ,易得
,易得![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() .
.
∴![]() .
.
当![]() ≤
≤![]() ,即
,即![]() 时,
时,
可类似地求得![]() ,这与
,这与![]() 矛盾,所以此时点P不存在.
矛盾,所以此时点P不存在.
∴旋转角![]() .
.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程  的一元二次方程
的一元二次方程 的两个整数根恰好比方程
的两个整数根恰好比方程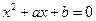 的两个根都大1,求
的两个根都大1,求 的值.
的值.  的一元二次方程x2+2x+m=0.
的一元二次方程x2+2x+m=0. 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围;