题目内容
【题目】在平面直角坐标系xOy中，对于点P与图形W,若点Q为图形W上任意一点，点Q关于第一、三象限角平分线的对称点为Q,且线段PQ,的中点为M（m,0）,则称点P是图形W关于点M（m,0）的“关联点”.
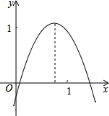
（1）如图1，若点P是点Q(0,
)关于原点的关联点，则点P的坐标为 ;
（2）如图2，在△ABC中，A（2,2），B（-2,0），C（0，-2），
①将线段AO向右平移d（d>0）个单位长度，若平移后的线段上存在两个△ABC关于点（2,0）的关联点，则d的取值范围是 .
②已知点S（n+2,0）和点T（n+4,0）,若线段ST上存在△ABC关于点N（n,0）的关联点，求n的取值范围.
【答案】（1）（
，0）；（2）①
；②
或
.
【解析】
（1）设P点坐标为（a，b），根据“关联点”的定义、中点的坐标公式和关于第一三象限角平分线对称的两点坐标规律即可求出；
（2）①先求出原AC与x轴的交点，然后根据△ABC是轴对称图形，且对称轴为第一、三象限角平分线和“关联点”的定义可得：“关联点”定义中Q为OA关于（2,0）的对称线段OA与△ABC边的交点，平移线段OA可发现：当A在C左侧，O过点（）或在（）右侧时符合题意，最后列不等式即可；
②由S、T的坐标可知：线段ST是x轴的一部分，线段ST关于N点的对称线段S T也是x轴的一部分，从而判断出定义中Q是△ABC边与x轴的交点，由图可知：点Q只有（-2，0）和（1,0）两种可能，再根据线段S T需过（-2，0）或（1,0）分类讨论并列不等式即可.
解：（1）设P点坐标为（a，b）
∵点Q关于第一、三象限角平分线的对称点为Q
∵根据关于第一三象限角平分线对称的两点坐标规律：点Q的横坐标为点Q的纵坐标，点Q的纵坐标为点Q的横坐标
∴点Q的坐标为：（
，0）
∴点P是点Q(0,)关于原点的关联点
∴P Q的中点为原点
∴
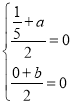
解得：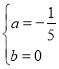
故P点坐标为：（，0）；
（2）设原AC的解析式为y=kx＋b
将A、C两点坐标代入：
解得：
∴原直线AC的解析式为：y=2x-2
当y=0时，解得：x=1
故原AC与x轴的交点为（1,0）
由图可知：△ABC是轴对称图形，且对称轴为第一、三象限角平分线
由“关联点”的定义可知：定义中Q在△ABC边上
∴点Q也在△ABC边上
∵将线段AO向右平移d（d>0）个单位长度，若平移后的线段上存在两个△ABC关于点（2,0）的关联点，
∴点Q和线段OA上的点必关于点（2,0）对称，此时O点坐标为（d，0），A点坐标为（2＋d，2）
故作出OA关于（2,0）的对称线段OA，其中O坐标为（4－d，0），A坐标为（2－d，－2），Q也必在OA上
即点Q为OA与△ABC边的交点，
∵线段上存在两个△ABC关于点（2,0）的关联点，
∴OA与△ABC边必须有两个交点才满足题意
如图中蓝线所示，平移OA可发现，当A与C重合时，与△ABC边有一个交点，继续向左平移即可有两个交点，当O过点（）也有两个交点，继续向左平移就只有一个交点
故当A在C左侧，O过点（）或在（）右侧时符合题意
∴
解得：.
②∵点S（n+2,0）和点T（n+4,0）
∴线段ST是x轴的一部分
∵线段ST上存在△ABC关于点N（n,0）的关联点
∴故S、T关于点N（n,0）的对称点S坐标为（n－2,0），T坐标为（n－4,0），定义中Q在线段S T上（x轴上），
∴Q即为△ABC边与x轴的交点
由图可知，点Q只有（-2，0）和（1,0）两种可能
∴线段S T需过（-2，0）或（1,0）
当S T过（-2，0）时
解得：；
当S T过（1，0）时
解得：.
综上所述：或.
