题目内容
将一枚六个面分别标有1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b.
(1)求点(a,b)落在直线y=2x-1上的概率;
(2)求以点O(0,0),A(4,-3),B(a,b)为顶点能构成等腰三角形的概率;
(3)求关于x,y的方程组
只有正数解的概率.
(1)求点(a,b)落在直线y=2x-1上的概率;
(2)求以点O(0,0),A(4,-3),B(a,b)为顶点能构成等腰三角形的概率;
(3)求关于x,y的方程组
|
分析:(1)找到落在落在直线y=2x-1的点即可;
(2)由题意知本题是一个古典概型,试验发生包含的事件数36种结果,而满足条件的事件是以点(0,0)、(1,-1)、(m,n)为顶点能构成等腰三角形,可以通过列举得到事件数,根据概率公式得到结果.
(3)列举出所有情况,看所求的情况占总情况的多少即可.
(2)由题意知本题是一个古典概型,试验发生包含的事件数36种结果,而满足条件的事件是以点(0,0)、(1,-1)、(m,n)为顶点能构成等腰三角形,可以通过列举得到事件数,根据概率公式得到结果.
(3)列举出所有情况,看所求的情况占总情况的多少即可.
解答:解:(1)列表得:
∵落在直线y=2x-1上的点有(1,1)、(2,3)、(3,5)三个,
∴点(a,b)落在直线y=2x-1上的概率为
=
;
(2)由题意知本题是一个古典概型,
试验发生包含的事件数36种结果,
而满足条件的事件是以点(0,0)、(4,-3)、(m,n)为顶点能构成等腰三角形,
(4,3)与(3,4),(4,2),(1,1),共有4种结果,
根据古典概型概率公式得到概率是
,
(3)当2a-b=0时,方程组无解;
当2a-b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.
易知a,b都为大于0的整数,则两式联合求解可得x=
,y=
,
∵使x、y都大于0则有
>0,
,>0,
∴解得a<1.5,b>3或者a>1.5,b<3,而a,b都为1到6的整数,
所以可知当a为1时b只能是4,5,6;或者a为2,3,4,5,6时b为1或2,
这两种情况的总出现可能有3+10=13种;
又掷两次骰子出现的基本事件共6×6=36种情况,故所求概率为
.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
∴点(a,b)落在直线y=2x-1上的概率为
| 3 |
| 36 |
| 1 |
| 12 |
(2)由题意知本题是一个古典概型,
试验发生包含的事件数36种结果,
而满足条件的事件是以点(0,0)、(4,-3)、(m,n)为顶点能构成等腰三角形,
(4,3)与(3,4),(4,2),(1,1),共有4种结果,
根据古典概型概率公式得到概率是
| 1 |
| 9 |
(3)当2a-b=0时,方程组无解;
当2a-b≠0时,方程组的解为由a、b的实际意义为1,2,3,4,5,6可得.
易知a,b都为大于0的整数,则两式联合求解可得x=
| 6-2b |
| 2a-b |
| 2a-3 |
| 2a-b |
∵使x、y都大于0则有
| 6-2b |
| 2a-b |
| 2a-3 |
| 2a-b |
∴解得a<1.5,b>3或者a>1.5,b<3,而a,b都为1到6的整数,
所以可知当a为1时b只能是4,5,6;或者a为2,3,4,5,6时b为1或2,
这两种情况的总出现可能有3+10=13种;
又掷两次骰子出现的基本事件共6×6=36种情况,故所求概率为
| 13 |
| 36 |
点评:本题考查了列表法或树状图求概率,第三题中难点是:当方程组相同未知数的系数之比相等,但与常数项之比不相等时,方程组无解,关键是得到使方程组为正整数的解的个数.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 x的图象上,小强获胜,若P(m,n)在函数y=
x的图象上,小强获胜,若P(m,n)在函数y=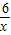 的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么?
的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么? x的图象上,小强获胜,若P(m,n)在函数y=
x的图象上,小强获胜,若P(m,n)在函数y=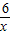 的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么?
的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么? x的图象上,小强获胜,若P(m,n)在函数y=
x的图象上,小强获胜,若P(m,n)在函数y=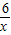 的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么?
的图象上,小兵获胜,你认为这个游戏规则是否公平?为什么?