题目内容
【题目】我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
（1）写出你所知道的四边形中是勾股四边形的两种图形的名称_____，_____；
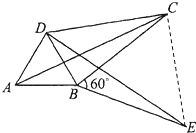
（2）如图，将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE，连接AD、DC，若∠DCB=30°，试证明；DC2+BC2=AC2．（即四边形ABCD是勾股四边形）
【答案】 直角梯形 矩形
【解析】试题分析：从平时的积累中我们就可以很快想到，直角梯形和矩形符合．然后根据图形作辅助线CE，看出
为等边三角形， 
为直角利用勾股定理进行解答即可．
试题解析：(1)∵直角梯形和矩形的角都为直角，所以它们一定为勾股四边形.
(2)证明：连接CE, 
∴△CBE为等边三角形，
又
∴△DCE为直角三角形
∵AC=DE，CE=BC,
练习册系列答案
相关题目
