题目内容
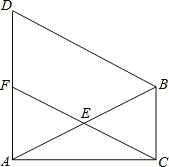
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.求证:
(1)△AEF≌△BEC;
(2)四边形BCFD是平行四边形.
【答案】证明见解析
【解析】
试题分析:(1)利用等边三角形的性质得出∠DAB=60°,即可得出∠ABC=60°,进而求出△AEF≌△BEC(ASA);
(2)利用平行线的判定方法以及直角三角形的性质得出CF∥BD,进而求出答案.
试题解析:(1)∵E是AB中点,∴AE=BE,
∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠ABC=60°,
在△AEF和△BEC中
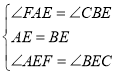 ,
,
∴△AEF≌△BEC(ASA);
(2)∵∠DAC=∠DAB+∠BAC,∠DAB=60°,∠CAB=30°,
∴∠DAC=90°,
∴AD∥BC,
∵E是AB的中点,∠ACB=90°,
∴EC=AE=BE,
∴∠ECA=30°,∠FEA=60°,
∴∠EFA=∠BDA=60°,
∴CF∥BD,
∴四边形BCFD是平行四边形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目