题目内容
如图，抛物线l1：y＝－x2－2x＋3交x轴于A、B两点，交y轴于M点，抛物线l1向右平移2个单位得到抛物线l2，l2交x轴于C、D两点．
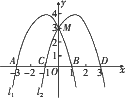
(1)求抛物线l2对应的函数表达式；
(2)抛物线l1或l2在x轴上方的部分是否存在点N，使以A、C、M、N为顶点的四边形是平行四边形．若存在，求出点N的坐标；若不存在，请说明理由．
答案：
解析：
解析：
|
解：(1)令y＝0，得－x2－2x＋3＝0， 所以x1＝－3，x2＝1． 所以A(－3，0)，B(1，0)． 因为抛物线l1向右平移2个单位得抛物线l2， 所以C(－1，0)，D(3，0)，a＝－1． 所以抛物线l2为y＝－(x＋1)(x－3)， 即y＝－x2＋2x＋3． (2)存在． 令x＝0，得y＝3，所以M(0，3)． 因为抛物线l2是l1向右平移2个单位得到的， 所以点N(2，3)在l2上，且MN＝2，MN∥AC． 又因为AC＝2，所以MN＝AC． 所以四边形ACNM为平行四边形． 同理，l1上的点 所以四边形ACM 所以N(2，3)， |
(－2，3)满足
练习册系列答案
相关题目
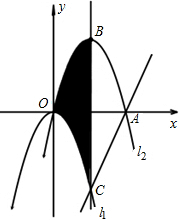如图，抛物线l1：y=-x2平移得到抛物线l2，且经过点O（0，0）和点A（4，0），l2的顶点为点B，它的对称轴与l2相交于点C，设l1、l2与BC围成的阴影部分面积为S，解答下列问题：
30、如图，抛物线L1：y=-x2-2x+3交x轴于A，B两点，交y轴于M点．将抛物线L1向右平移2个单位后得到抛物线L2，L2交x轴于C，D两点．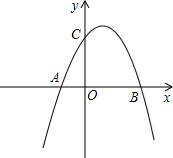
如图，抛物线L1：y=-x2-4x+5交x轴于A、B，交y轴于C，顶点为D．
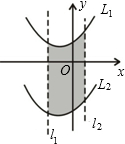如图将抛物线L1：y=x2+2x+3向下平移10个单位得L2，而l1、l2的表达式分别是l1：x=-2，l2：
如图，抛物线l1：y1=a（x+1）2+2与l2：y2=-（x-2）2-1交于点B（1，-2），且分别与y轴交于点D、E．过点B作x轴的平行线，交抛物线于点A、C，则以下结论：