题目内容
已知变量y与x成反比例,它的图象过点A(-2,3).求:
(1)反比例函数解析式
(2)从A(-2,3)向x轴和y轴分别作垂线AB、AC,垂足分别为B、C,则矩形OBAC的面积为
(3)当A点的横坐标为-4时,作AB1、AC1分别垂直于x轴、y轴,B1、C1为垂足,则所得矩形OB1AC1的面积是
(4)将A点在图象上任意移动到点A′,作A′B′、A′C′分别垂直于x轴、y轴,B′、C′为垂足,则所得矩形OB′A′C′的面积是
由此,你可以结合上述信息得出结论是:
(1)反比例函数解析式
(2)从A(-2,3)向x轴和y轴分别作垂线AB、AC,垂足分别为B、C,则矩形OBAC的面积为
6
6
.(3)当A点的横坐标为-4时,作AB1、AC1分别垂直于x轴、y轴,B1、C1为垂足,则所得矩形OB1AC1的面积是
6
6
.(4)将A点在图象上任意移动到点A′,作A′B′、A′C′分别垂直于x轴、y轴,B′、C′为垂足,则所得矩形OB′A′C′的面积是
6
6
.由此,你可以结合上述信息得出结论是:
|K|
|K|
.分析:(1)利用变量y与x成反比例,它的图象过点A(-2,3),直接代入y=
,求出即可;
(2)利用图象上点的性质以及矩形面积求法得出即可;
(3)利用(2)中所求方法,即可得出矩形面积;
(4)利用以上面积求法即可得出矩形OB′A′C′的面积以及规律.
| k |
| x |
(2)利用图象上点的性质以及矩形面积求法得出即可;
(3)利用(2)中所求方法,即可得出矩形面积;
(4)利用以上面积求法即可得出矩形OB′A′C′的面积以及规律.
解答:解:(1)∵y与x成反比例,它的图象过点A(-2,3),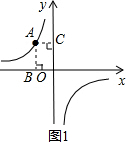
代入y=
,∴k=xy=-6,
∴y=
;
(2)如图1:
∵从A(-2,3)向x轴和y轴分别作垂线AB、AC,垂足分别为B、C,
∴AC=2,AB=3,
∴矩形OBAC的面积为:2×3=6;
(3)如图2,
∵A点的横坐标为-4,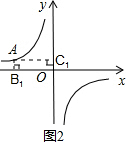
∴A点的纵坐标为:y=
=
,
∴AB1=
,AC1=4,
∴矩形OB1AC1的面积是:4×
=6;
(4)同理可得出,A点在图象上任意移动到点A′,作A′B′、A′C′分别垂直于x轴、y轴,B′、C′为垂足,
则所得矩形OB′A′C′的面积是:6,
∴反比例函数图象上的点向坐标轴作垂线与坐标轴围成的矩形的面积是定值,大小为|k|.

代入y=
| k |
| x |
∴y=
| -6 |
| x |
(2)如图1:
∵从A(-2,3)向x轴和y轴分别作垂线AB、AC,垂足分别为B、C,
∴AC=2,AB=3,
∴矩形OBAC的面积为:2×3=6;
(3)如图2,
∵A点的横坐标为-4,

∴A点的纵坐标为:y=
| -6 |
| -4 |
| 3 |
| 2 |
∴AB1=
| 3 |
| 2 |
∴矩形OB1AC1的面积是:4×
| 3 |
| 2 |
(4)同理可得出,A点在图象上任意移动到点A′,作A′B′、A′C′分别垂直于x轴、y轴,B′、C′为垂足,
则所得矩形OB′A′C′的面积是:6,
∴反比例函数图象上的点向坐标轴作垂线与坐标轴围成的矩形的面积是定值,大小为|k|.
点评:此题主要考查了反比例函数的性质以及矩形面积求法,根据已知结合图象得出是解题关键.

练习册系列答案
相关题目