题目内容
如图1,过平行四边形纸片的一个顶点作它的一条垂线段h,沿这条垂线段剪下三角形纸片,将它平移到右边,平移距离等于平行四边形的底边长a.(1)平移后的图形是矩形吗?为什么?
(2)图2中,BD是平移后的四边形ABCD的对角线,F为AD上一点,CF交BD于点G,CE⊥BD于点E,求证:∠2=∠1+∠3.
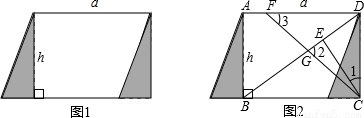
【答案】分析:(1)因为是平移,那么首先平移后的四边形应该是平行四边形,又因为h与上下两边垂直,平移后的图形是矩形;
(2)本题可用等角转换来得出结论,∠2是三角形BGC的外角,那么∠2=∠DBC+∠GCB,根据AD∥BC,可得出∠3=∠GCB,根据∠1和∠DBC都和∠CDB互余,可得出∠1=∠DBC,由此可得出本题的结论.
解答:(1)解:是矩形,因为平移后的图形首先是个平行四边形,又因为这个平行四边形的相邻的两边都垂直,因此是个矩形.
(2)证明:∵AD∥BC,
∴∠3=∠GCB.
∵∠1+∠CDB=90°,∠DBC+∠CDB=90°,
∴∠1=∠DBC.
∵∠2=∠DBC+∠GCB,
∴∠2=∠1+∠3.
点评:本题主要是对平行四边形的性质及平移性质和互为余(补)角的等知识的直接考查.
(2)本题可用等角转换来得出结论,∠2是三角形BGC的外角,那么∠2=∠DBC+∠GCB,根据AD∥BC,可得出∠3=∠GCB,根据∠1和∠DBC都和∠CDB互余,可得出∠1=∠DBC,由此可得出本题的结论.
解答:(1)解:是矩形,因为平移后的图形首先是个平行四边形,又因为这个平行四边形的相邻的两边都垂直,因此是个矩形.
(2)证明:∵AD∥BC,
∴∠3=∠GCB.
∵∠1+∠CDB=90°,∠DBC+∠CDB=90°,
∴∠1=∠DBC.
∵∠2=∠DBC+∠GCB,
∴∠2=∠1+∠3.
点评:本题主要是对平行四边形的性质及平移性质和互为余(补)角的等知识的直接考查.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
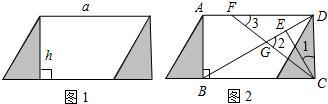 23、如图1,过平行四边形纸片的一个顶点作它的一条垂线段h,沿这条垂线段剪下三角形纸片,将它平移到右边,平移距离等于平行四边形的底边长a.
23、如图1,过平行四边形纸片的一个顶点作它的一条垂线段h,沿这条垂线段剪下三角形纸片,将它平移到右边,平移距离等于平行四边形的底边长a. 22、如图,EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F,已知AB=4,BC=5,OE=1.5,那么四边形EFCD的周长是
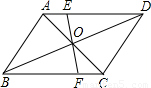
22、如图,EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F,已知AB=4,BC=5,OE=1.5,那么四边形EFCD的周长是 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是