题目内容
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
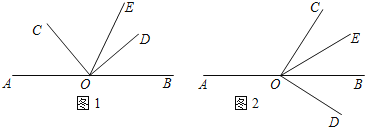
(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
【答案】(1)20°;(2)综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB
【解析】
(1)依据邻补角的定义以及角平分线的定义,即可得到∠COE的度数,进而得出∠DOE的度数;
(2)设∠AOC=α,则∠BOC=180°-α,依据OE平分∠BOC,可得∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
(1)∵∠AOC=40°,
∴∠BOC=140°,
又∵OE平分∠BOC,
∴∠COE=![]() ×140°=70°,
×140°=70°,
∵∠COD=90°,
∴∠DOE=90°-70°=20°;
(2)设∠AOC=α,则∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,
α,
分两种情况:
当OD在直线AB上方时,∠BOD=90°-α,
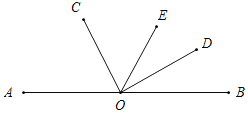
∵∠COE=2∠DOB,
∴90°-![]() α=2(90°-α),
α=2(90°-α),
解得α=60°.
当OD在直线AB下方时,∠BOD=90°-(180°-α)=α-90°,
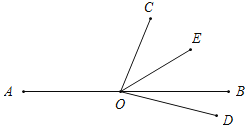
∵∠COE=2∠DOB,
∴90°-![]() α=2(α-90°),
α=2(α-90°),
解得α=108°.
综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB.

练习册系列答案
相关题目







