ƒøƒ⁄»ð
°æƒø°ø∂®“£∫¡ΩÃı≥§∂»œýµ»£¨«“À¸√«À˘‘⁄µƒ÷±œþª•œý¥π÷±µƒœþ∂Œ£¨Œ“√«≥∆∆‰ª•Œ™°∞µ»¥πœþ∂Œ°±£Æ
÷™ ∂”¶”√£∫‘⁄°˜ABC∫Õ°˜ADE÷–£¨AC=BC£¨AE=DE£¨«“AE<AC£¨ °œACB=°œAED=90°„£¨¡¨Ω”BD£¨µ„P «œþ∂ŒBDµƒ÷–µ„£¨¡¨Ω”PC£¨PE£Æ
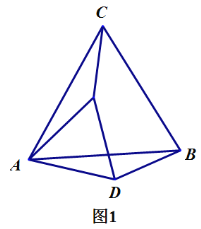
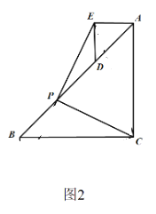
£®1£©»ÁÕº1£¨µ±AE‘⁄œþ∂ŒAC…œ ±£¨œþ∂ŒPC”Îœþ∂ŒPE «∑Òª•Œ™°∞µ»¥πœþ∂Œ°±£ø«ÎÀµ√˜¿Ì”…£Æ
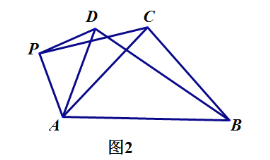
£®2£©»ÁÕº2£¨Ω´Õº1÷–µƒ°˜ADE»∆µ„AÀ≥ ±’Ζ˝◊™90°„£¨µ„D¬‰‘⁄AB±þ…œ£¨«ÎÀµ√˜œþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£Æ
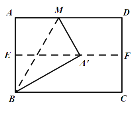
Õÿ’π—”…Ï£∫£®3£©Ω´Õº1÷–µƒ°˜ADE»∆µ„AÀ≥ ±’Ζ˝◊™150°„£¨»ÙBC=3£¨DE=1£¨«ÛPCµƒ÷µ£Æ

°æ¥∞∏°ø£®1£©œþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£¨¿Ì”…º˚Ω‚Œˆ£ª£®2£©º˚Ω‚Œˆ£ª£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©—”≥§EPΩªBC”⁄µ„F£¨ ◊œ»÷§√˜![]() £¨‘Ú”–PF=PE=
£¨‘Ú”–PF=PE=![]() EF£¨BF=DE£¨»ª∫Û÷§√˜°˜EFC «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘Ÿ¿˚”√µ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ º¥ø…÷§√˜œþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£ª
EF£¨BF=DE£¨»ª∫Û÷§√˜°˜EFC «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘Ÿ¿˚”√µ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ º¥ø…÷§√˜œþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£ª
£®2£©◊˜BF//DE£¨ΩªEPµƒ—”≥§œþ”⁄µ„F£¨¡¨Ω”CE£¨CF£¨ ◊œ»÷§√˜![]() £¨‘Ú”–BF= DE£¨ PE=PF=
£¨‘Ú”–BF= DE£¨ PE=PF=![]() EF£¨»ª∫Û¿˚”√∆Ω––œþµƒ–‘÷ µ√≥ˆ°œCBF=°œCAE£¨Ω¯∂¯ø…÷§
EF£¨»ª∫Û¿˚”√∆Ω––œþµƒ–‘÷ µ√≥ˆ°œCBF=°œCAE£¨Ω¯∂¯ø…÷§![]() £¨‘Ú”–CF=CE£¨°œFCB=°œECA£¨¥”∂¯µ√≥ˆ°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘ÚΩ·¬€ø…÷§£ª
£¨‘Ú”–CF=CE£¨°œFCB=°œECA£¨¥”∂¯µ√≥ˆ°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘ÚΩ·¬€ø…÷§£ª
£®3£©◊˜BF//DE£¨ΩªEPµƒ—”≥§œþ”⁄µ„F£¨¡¨Ω”CE£¨CF£¨π˝µ„E◊˜EH°ÕACΩªCAµƒ—”≥§œþ”⁄µ„H£¨ ◊œ»÷§√˜![]() £¨‘Ú”–BF= DE£¨ PE=PF=
£¨‘Ú”–BF= DE£¨ PE=PF=![]() EF£¨»ª∫Ûø…÷§
EF£¨»ª∫Ûø…÷§![]() £¨‘Ú”–CF=CE£¨°œFCB=°œECA£¨¥”∂¯µ√≥ˆ°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘ÚPC=PE=
£¨‘Ú”–CF=CE£¨°œFCB=°œECA£¨¥”∂¯µ√≥ˆ°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£¨‘ÚPC=PE=![]() EC£¨»ª∫Û‘⁄Rt
EC£¨»ª∫Û‘⁄Rt![]() AHE÷–£¨«Û≥ˆHE,AHµƒ≥§∂»£¨Ω¯∂¯«Û≥ˆCHµƒ≥§∂»£¨»ª∫Û‘⁄Rt
AHE÷–£¨«Û≥ˆHE,AHµƒ≥§∂»£¨Ω¯∂¯«Û≥ˆCHµƒ≥§∂»£¨»ª∫Û‘⁄Rt![]() CEH÷–£¨”…π¥π…∂®¿Ì«Û≥ˆECµƒ≥§∂»£¨‘ÚPCµƒ≥§∂»ø…«Û £Æ
CEH÷–£¨”…π¥π…∂®¿Ì«Û≥ˆECµƒ≥§∂»£¨‘ÚPCµƒ≥§∂»ø…«Û £Æ
Ω‚£∫(1)œþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£Æ
¿Ì”…£∫»ÁÕº1£¨—”≥§EPΩªBC”⁄µ„F£Æ
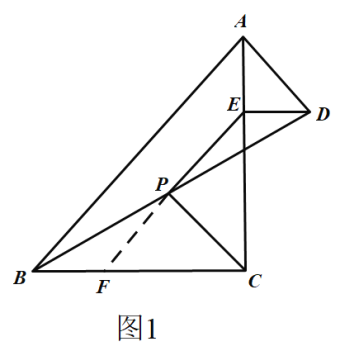
°þ°œACB=°œAED=90°„£¨
°ýDE![]() BC£¨
BC£¨
°ý°œEDP=°œFBP£Æ
°þµ„P «œþ∂ŒBDµƒ÷–µ„£¨
°ýPB=PD£Æ
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨
![]()
°ýPF=PE=![]() EF£¨BF=DE£Æ
EF£¨BF=DE£Æ
°þAC=BC£¨AE=DE£¨
°ýAC©ÅAE=BC©ÅBF£¨º¥EC=FC£Æ
”÷°þ°œACB=90°„£¨
°ý°˜EFC «µ»—¸÷±Ω«»˝Ω«–Œ£Æ
°þEP=FP£¨
°ýPC=PE£¨PC°ÕPE£¨
°ýœþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£ª
£®2£©»ÁÕº2£¨◊˜BF//DE£¨ΩªEPµƒ—”≥§œþ”⁄µ„F£¨¡¨Ω”CE£¨CF£¨
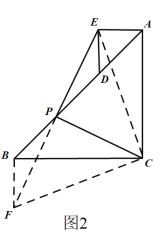
°þDE![]() BF£¨
BF£¨
°ý°œEDP=°œFBP£Æ
°þµ„P «œþ∂ŒBDµƒ÷–µ„£¨
°ýPB=PD£Æ
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨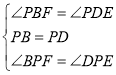
![]()
°ýBF= DE£¨ PE=PF=![]() EF£Æ
EF£Æ
°þDE=AE£¨
°ýBF=AE£Æ
°þ°œCAE=90°„£¨°œAED=90°„£¨
°ýED![]() AC£Æ
AC£Æ
![]() £¨
£¨
°ýFB![]() AC£¨
AC£¨
°ý![]() £¨
£¨
°ý°œCBF=°œCAE£Æ
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨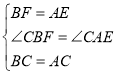
![]()
°ýCF=CE£¨°œFCB=°œECA£Æ
°þ°œACB=90°„£¨
°ý°œFCE=90°„£¨
°ý°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£Æ
°þPE=PF£¨
°ýPC°ÕPE£¨PC=PE£¨
°ýœþ∂ŒPC”Îœþ∂ŒPEª•Œ™°∞µ»¥πœþ∂Œ°±£ª
(3)»ÁÕº3
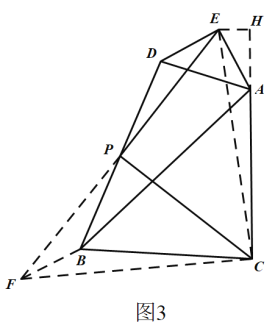
◊˜BF//DE£¨ΩªEPµƒ—”≥§œþ”⁄µ„F£¨¡¨Ω”CE£¨CF£¨π˝µ„E◊˜EH°ÕACΩª
µ±–˝◊™Ω«Œ™150°„ ±£¨”…–˝◊™ø…÷™£¨°œCAE=150°„£¨DE”ÎBCÀ˘º–µƒ»ÒΩ«Œ™30°„£¨
°ý°œFBC=°œEAC=150°„£Æ
°þDE![]() BF£¨
BF£¨
°ý°œEDP=°œFBP£Æ
°þµ„P «œþ∂ŒBDµƒ÷–µ„£¨
°ýPB=PD£Æ
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨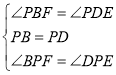
![]()
°ýBF= DE£¨ PE=PF=![]() EF£Æ
EF£Æ
°þDE=AE £¨
°ýBF=AE£Æ
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨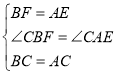
![]()
°ýCF=CE£¨°œFCB=°œECA£Æ
°þ°œACB=90°„ £¨
°ý°œFCE=90°„£¨
°ý°˜FCE «µ»—¸÷±Ω«»˝Ω«–Œ£Æ
°þPE=PF£¨
°ýPC°ÕPE£¨PC=PE=![]() EC£Æ
EC£Æ
‘⁄Rt![]() AHE÷–£¨°œEAH=30°„£¨AE=DE=1£¨
AHE÷–£¨°œEAH=30°„£¨AE=DE=1£¨
°ýHE=![]() £¨AH=
£¨AH=![]() £Æ
£Æ
”÷°þAC=BC=3£¨
°ýCH=AC+AH=3+![]() £Æ
£Æ
‘⁄Rt![]() CEH÷–£¨
CEH÷–£¨
”…π¥π…∂®¿Ìµ√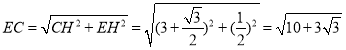 £¨
£¨
![]() £Æ
£Æ

 ª∆∏‘–°◊¥‘™Ω‚戌 ÂÃÏÃÏ¡∑œµ¡–¥∞∏
ª∆∏‘–°◊¥‘™Ω‚戌 ÂÃÏÃÏ¡∑œµ¡–¥∞∏ »˝µ„“ª≤‚øÏ¿÷÷к∆ªÆœµ¡–¥∞∏
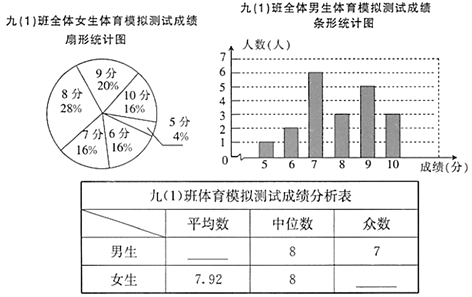
»˝µ„“ª≤‚øÏ¿÷÷к∆ªÆœµ¡–¥∞∏°æƒø°øƒ≥ –∂‘º¥Ω´≤Œº”÷–øºµƒ4000√˚≥ı÷–±œ“µ…˙Ω¯––¡À“ª¥Œ ”¡¶≥È—˘µ˜≤È£¨ªÊ÷∆≥ˆ∆µ ˝∑÷≤º±Ì∫Õ≤ªÕÍ’˚µƒ∆µ ˝∑÷≤º÷±∑ΩÕº£Æ«Î∏˘æðÕº±Ì–≈œ¢ªÿ¥œ¬¡–Œ £∫
≥ı÷–±œ“µ…˙ ”¡¶≥È—˘µ˜≤È∆µ ˝∑÷≤º±Ì
”¡¶ | ∆µ ˝£®»À£© | ∆µ¬ |
4.0°Ðx£º4.3 | 20 | 0.1 |
4.3°Ðx£º4.6 | 40 | 0.2 |
4.6°Ðx£º4.9 | 70 | 0.35 |
4.9°Ðx£º5.2 | a | 0.3 |
5.2°Ðx£º5.5 | 10 | b |

£®1£©±æ¥Œµ˜≤È—˘±æ»ð¡øŒ™°° °°£ª
£®2£©‘⁄∆µ ˝∑÷≤º±Ì÷–£¨a£Ω °°£¨b£Ω°° °°£¨≤¢Ω´∆µ ˝∑÷≤º÷±∑ΩÕº≤π≥‰ÕÍ’˚£ª
£®3£©»Ù ”¡¶‘⁄4.9“‘…œ£®∫¨4.9£©æ˘ Ù±Í◊º ”¡¶£¨∏˘æð…œ ˆ–≈œ¢π¿º∆»´«¯≥ı÷–±œ“µ…˙÷–¥ÔµΩ±Í◊º ”¡¶µƒ—ß…˙‘º”–∂ý…Ÿ»À£ø