题目内容
若反比例函数 的图象在第二、四象限,则m= .
的图象在第二、四象限,则m= .
【答案】分析:根据反比例函数的定义先求出m的值,再根据反比例函数的性质即可求解.
解答:解:由题意可知:m2-5=-1,m+1≠0,
∴m=±2,
∵该函数的图象在第二、四象限内.
∴m+1<0,
∴m=-2,
故答案为-2.
点评:本题主要考查反比例函数的性质和定义的知识点,首先将反比例函数解析式的一般式 (k≠0),转化为y=kx-1(k≠0)的形式,根据反比例函数的定义条件可以求出m的值;
(k≠0),转化为y=kx-1(k≠0)的形式,根据反比例函数的定义条件可以求出m的值;
特别注意不要忽略k≠0这个条件.并且反比例函数图象所在的象限,是由反比例系数k的符号确定.
解答:解:由题意可知:m2-5=-1,m+1≠0,
∴m=±2,
∵该函数的图象在第二、四象限内.
∴m+1<0,
∴m=-2,
故答案为-2.
点评:本题主要考查反比例函数的性质和定义的知识点,首先将反比例函数解析式的一般式
 (k≠0),转化为y=kx-1(k≠0)的形式,根据反比例函数的定义条件可以求出m的值;
(k≠0),转化为y=kx-1(k≠0)的形式,根据反比例函数的定义条件可以求出m的值;特别注意不要忽略k≠0这个条件.并且反比例函数图象所在的象限,是由反比例系数k的符号确定.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 的图象在每个象限内
的图象在每个象限内 的值随
的值随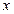 值的增大而增大,则
值的增大而增大,则 的取值范围是
的取值范围是



 的图象在第一、三象限,则k的取值范围是____________
的图象在第一、三象限,则k的取值范围是____________ 的图象在各个象限内
的图象在各个象限内 随着
随着 的增大而增大,则
的增大而增大,则 的取值范围是( ▲ )
的取值范围是( ▲ ) B.
B. C.
C. D.
D.