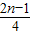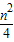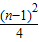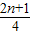题目内容
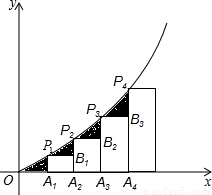
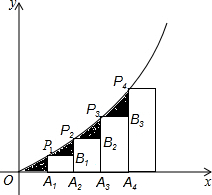 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:把x=n和x=n-1代入二次函数求出y的值,即可求出三角形的边长,根据面积公式计算即可.
解答:解:二次函数y=
x2,由图象知:
当x=n时,y=
n2,
当x=n-1时,y=
(n-1)2,
∴Sn=
×1×[
n2-
(n-1)2],
=
.
故选A.
| 1 |
| 2 |
当x=n时,y=
| 1 |
| 2 |
当x=n-1时,y=
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 2n-1 |
| 4 |
故选A.
点评:本题主要考查了二次函数的点的坐标特征,三角形的面积等知识点,解此题的关键是求出三角形的边长.

练习册系列答案
相关题目
 x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )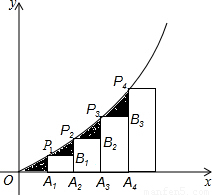
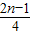
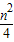
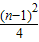
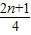
 x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )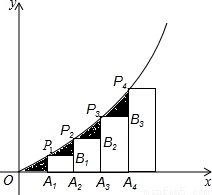
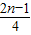
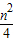
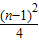
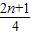
 x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )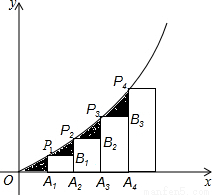
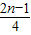
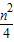
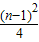
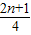
 x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )