题目内容
南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
解:(1)由题意得:y=29﹣25﹣x,
∴y=﹣x+4(0≤x≤4);
(2)z=(8+ ×4)y
×4)y
=(8x+8)(﹣x+4)
∴z=﹣8x2+24x+32
=﹣8(x﹣ )2+50
)2+50
(3)由第二问的关系式可知:当x= 时,z最大=50
时,z最大=50
∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元
或:当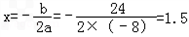
z最大值=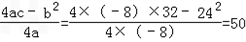
∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元。
∴y=﹣x+4(0≤x≤4);
(2)z=(8+
 ×4)y
×4)y =(8x+8)(﹣x+4)
∴z=﹣8x2+24x+32
=﹣8(x﹣
 )2+50
)2+50 (3)由第二问的关系式可知:当x=
 时,z最大=50
时,z最大=50 ∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元
或:当
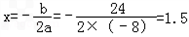
z最大值=
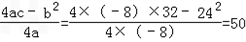
∴当定价为29﹣1.5=27.5万元时,有最大利润,最大利润为50万元。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价) 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为 万元.(销售利润
万元.(销售利润 销售价
销售价 进货价)
进货价) 万元,试写出
万元,试写出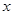 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为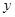 万元.(销售利润
万元.(销售利润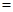 销售价
销售价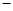 进货价)
进货价)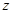 万元,试写出
万元,试写出