题目内容
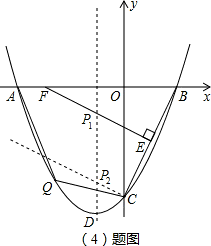
如图①,抛物线y= x2+x-4与x轴的两个交点分别为A、B,与y轴的交点为C.
x2+x-4与x轴的两个交点分别为A、B,与y轴的交点为C.
(1)请直接写出点A、B、C的坐标;
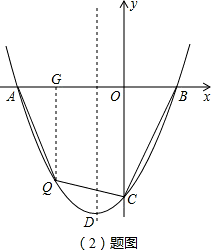
(2)如图①,点Q是函数y= x2+x-4的图象在第三象限上的任一点,点Q的横坐标为m,设四边形AQCB的面积为S,求S与m之间的函数关系式,并求出m这何值时,S有最大值,最大值是多少?
x2+x-4的图象在第三象限上的任一点,点Q的横坐标为m,设四边形AQCB的面积为S,求S与m之间的函数关系式,并求出m这何值时,S有最大值,最大值是多少?
(3)抛物线y= x2+x-4的对称轴上是否存在一点H,使△BCH的周长最小?若存在,请直接写出H点坐标;若不存在,请说明理由.
x2+x-4的对称轴上是否存在一点H,使△BCH的周长最小?若存在,请直接写出H点坐标;若不存在,请说明理由.
(4)如图②,若点E为线段BC的中点,EF垂直平分BC交x轴于点F(-3,0),点P是抛物线y= x2+x-4对称轴上的一点,设P点的纵坐标为t,请直接写出∠PEC为钝角三角形时t的取值范围.
x2+x-4对称轴上的一点,设P点的纵坐标为t,请直接写出∠PEC为钝角三角形时t的取值范围.
 解:(1)抛物线y=
解:(1)抛物线y= x2+x-4中,
x2+x-4中,令x=0,y=-4,即 C(0,-4);
令y=0,
 x2+x-4=0,解得:x1=2、x2=-4,即 A(-4,0)、B(2,0).
x2+x-4=0,解得:x1=2、x2=-4,即 A(-4,0)、B(2,0).(2)如右图,过点Q作QG⊥x轴于G,则 Q(m,
 m2+m-4),OG=-m,AG=0A=4-(-m)=4+m,QG=-
m2+m-4),OG=-m,AG=0A=4-(-m)=4+m,QG=- m2-m+4;
m2-m+4;S=S△AQG+S梯形GQCO+S△OBC
=
 ×(4+m)×(-
×(4+m)×(- m2-m+4)+
m2-m+4)+ ×(-
×(- m2-m+4+4)×(-m)+
m2-m+4+4)×(-m)+ ×2×4
×2×4=-m2-4m+12
=-(m+2)2+16,
∴当m=-2时,S有最大值,且Smax=16.
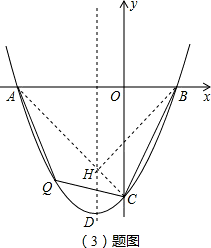
(3)如右图,点A、B关于抛物线的对称轴对称,所以当△BCH的周长最短时,点H为直线AC与抛物线对称轴的交点;
设直线AC的解析式:y=kx+b,代入A(-4,0)、C(0,-4),有:
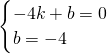 ,解得
,解得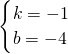
∴直线AC:y=-x-4;
由(1)知,抛物线的对称轴:x=-
 =-1;
=-1;∴当x=-1时,y=1-4=-3,即当H(-1,-3)时,△BCH的周长最小.
(4)如右图,分三种情况讨论:
①当点P为直线EF与抛物线对称轴交点时;
已知点E为线段BC的中点,则E(1,-2),又由F(-3,0),可求得:
 直线EF:y=-
直线EF:y=- x-
x- ,则P1(-1,-1),t=-1;
,则P1(-1,-1),t=-1;②当CP⊥BC,且P为CP与抛物线对称轴交点时;
此时,CP2∥EF,设直线CP2:y=-
 x+b,代入C(0,-4),得:
x+b,代入C(0,-4),得:直线CP2:y=-
 x-4,则P2(-1,-
x-4,则P2(-1,- ),t=-
),t=- ;
;③当CP3⊥EP3时,设P3(-1,t),则:
EP32=(1+1)2+(-2-t)2=t2+4t+8,CP32=1+(-4-t)2=t2+8t+17,EC2=5;
在Rt△EP3C中,EP32+CP32=EC2,即:
t2+4t+8+t2+8t+17=5,
化简,得:t2+6t+10=0,此方程无解,这种情况不成立;
综上,当t>-1或t<-
 时,△ECP为钝角三角形.
时,△ECP为钝角三角形.分析:(1)抛物线的解析式中,令x=0,可求得点C的坐标;令y=0,可求得点A、B的坐标.
(2)过点Q作QG⊥x轴于G,将四边形AQCB分作△AQG、梯形GQCO、△OBC三部分,设出点Q的坐标后,用m表达出上述三部分的面积和,即可得到关于S、m的函数关系式,根据函数的性质即可求出S的最大值及对应的m的值.
(3)△BCH的周长中,BC的长是定值,若△BCH的周长最短,那么BH+CH的长最短;点A、B关于抛物线的对称轴对称,那么直线AC与抛物线对称轴的交点即为符合条件的点H.
(4)此题需要考虑三种情况:①当P为直线EF与抛物线对称轴的交点时t的值;②当P为过点C且与直线BC垂直的直线与抛物线对称轴的交点时t的值;③当P为Rt△PEC的直角顶点时t的值;结合图形和上时三种情况来讨论△PEC为钝角三角形时t的取值范围.
点评:此题主要考查了:图形面积的求法、二次函数的应用、轴对称图形的性质与两点间线段最短的综合应用、直角三角形以及钝角三角形的特点等重要知识,涵盖了二次函数综合题中多类常考题型.最后一题中,找出△ECP是直角三角形时t的值(共三种情况)是解答题目的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=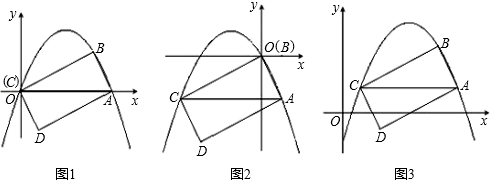
 如图,将抛物线
如图,将抛物线