题目内容
顺次连接对角线相等的四边形四边中点所得的四边形是 ( )
| A.梯形 | B.菱形 | C.矩形 | D.正方形 |
B
画出图形,由三角形中位线的性质,再根据有一组邻边相等的平行四边形是菱形得出答案.
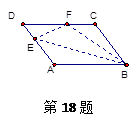
已知,如图:

E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,对角线AC=BD,
求证:四边形EFGH是菱形.
证明:∵E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
又∵EF= AC,EH=
AC,EH= AC,AC=BD,
AC,AC=BD,
∴EH=EF,
∴平行四边形EFGH是菱形,
∴四边形EFGH是菱形.
故选B.
菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.
已知,如图:

E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,对角线AC=BD,
求证:四边形EFGH是菱形.
证明:∵E、F、G、H分别是四边形ABCD各边AB、BC、CD、DA的中点,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
又∵EF=
 AC,EH=
AC,EH= AC,AC=BD,
AC,AC=BD,∴EH=EF,
∴平行四边形EFGH是菱形,
∴四边形EFGH是菱形.
故选B.
菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




 ),计算两圆孔中心
),计算两圆孔中心 和
和 的距离为______
的距离为______
 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点 在正方形
在正方形 上有一点
上有一点 ,使
,使 的和最小,则这个最小值为 .
的和最小,则这个最小值为 .

 是正方形,点
是正方形,点 在
在 上,
上, 于
于 ,请你在
,请你在 上确定一点
上确定一点 ,使
,使 ,并说明理由。
,并说明理由。