题目内容
某工厂生产A、B两种产品共50件,其生产成本与利润如下表:
若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?
| | A种产品 | B种产品 |
| 成本 (万元/件) | 0.6 | 0.9 |
| 利润 (万元/件) | 0.2 | 0.4 |
若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?
解:设生产A种产品x件,则B种产品为50-x件,
根据题意有: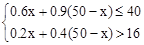
不等式组的解集为: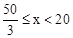 。
。
∵x为整数,∴x=17或18或19。
生产方案如下:①生产A种产品17件,生产B种产品33件;
②生产A种产品18件,生产B种产品32件;
③生产A种产品19件,生产B种产品31件。
设利润为W,则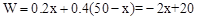 ,
,
∵-0.2<0,∴W随x的增大而减小。∴当x=17时,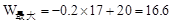 。
。
答:工厂有三种生产方案:①生产A种产品17件,生产B种产品33件;②生产A种产品18件,生产B种产品32件;③生产A种产品19件,生产B种产品31件。方案①获利润最大,最大利润是16.6万元。
根据题意有:
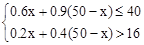
不等式组的解集为:
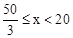 。
。∵x为整数,∴x=17或18或19。
生产方案如下:①生产A种产品17件,生产B种产品33件;
②生产A种产品18件,生产B种产品32件;
③生产A种产品19件,生产B种产品31件。
设利润为W,则
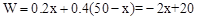 ,
,∵-0.2<0,∴W随x的增大而减小。∴当x=17时,
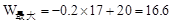 。
。答:工厂有三种生产方案:①生产A种产品17件,生产B种产品33件;②生产A种产品18件,生产B种产品32件;③生产A种产品19件,生产B种产品31件。方案①获利润最大,最大利润是16.6万元。
一元一次不等式组和一次函数的应用。
【分析】根据题目的已知条件建立不等式组的数学模型和一次函数的数学模型求解。
【分析】根据题目的已知条件建立不等式组的数学模型和一次函数的数学模型求解。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目

 ,
, 与
与 成正比例,
成正比例, 与
与 时,
时, ;当
;当 时,
时, .(1)求
.(1)求 与
与 时,求
时,求 的图象经过第_____________________象限 ( )
的图象经过第_____________________象限 ( ) 是关于x的一次函数,且y随x的增大而增大,则m =___ _。
是关于x的一次函数,且y随x的增大而增大,则m =___ _。