题目内容
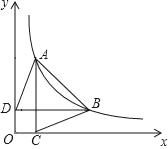
【题目】如图,已知双曲线y=![]() (x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(1)若A、B两点的坐标分别是(1,4)、(4,1),求S△OAB;
(2)证明:S△ABD=S△ABC.
(3)连接CD,判断CD与AB的位置关系,并说明理由.
【答案】(1)见解析;(2)见解析;(3)CD∥AB,理由见解析
【解析】
(1)作BH⊥x轴于H,如图,利用图形得到S△OAB+S△OBH=S△AOC+S梯形ACHB,根据反比例函数k的几何意义得S△OBH=S△AOC,所以S△OAB=S梯形ACHB,然后根据梯形得面积公式求解;
(2)根据反比例函数图象上点的坐标特征,设A(a,![]() ),B(b,
),B(b,![]() ),然后根据三角形面积公式可得S△ABD=S△ABC=
),然后根据三角形面积公式可得S△ABD=S△ABC=![]() k;
k;
(3)由于S△ABD=S△ABC,根据三角形面积公式得到点C点和点D到AB的距离相等,所以CD∥AB.
(1)解:作BH⊥x轴于H,如图,
∵S△OAB+S△OBH=S△AOC+S梯形ACHB,
而S△OBH=S△AOC,
∴S△OAB=S梯形ACHB=![]() ×(1+4)×(4﹣1)=
×(1+4)×(4﹣1)=![]() ;
;
(2)证明:设A(a,![]() ),B(b,
),B(b,![]() ),
),
∵S△ABD=![]() b(
b(![]() ﹣
﹣![]() )=
)=![]() k,
k,
S△ABC=![]()
![]() (b﹣a)=
(b﹣a)=![]() k,
k,
∴S△ABD=S△ABC;
(3)解:CD∥AB.理由如下:
∵S△ABD=S△ABC,
∴CD∥AB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目