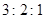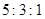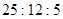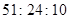题目内容
(8分)若矩形的一个短边与长边的比值为 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1) 操作:请你在如图15所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD。
(2) 探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由。
(3) 归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)
 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形(1) 操作:请你在如图15所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD。
(2) 探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由。
(3) 归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)

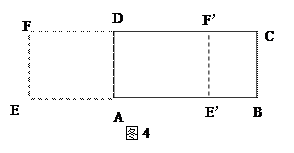
解(1)以AD为边可作出两个正方形AEFD与AE′F′D′(AB>AD),如图4所示
(2)矩形EBCF不是黄金矩形,理由如下:
设AB=a,AD=b(a>b),则BE=BA+AE=a+b,BE′=BA-E′A=a-b,
由ABCD为黄金矩形,得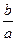 =
=
∴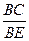 =
=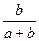 =
=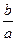 ÷(1+
÷(1+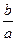 )=
)= ÷(1+
÷(1+ )=
)=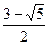 ≠
≠
∴矩形EBCF不是黄金矩形
矩形E′BCF′是黄金矩形
证明:如图4,∵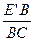 =
=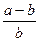 =(1-
=(1-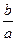 )÷
)÷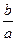 =(1-
=(1- )÷
)÷ =
=
∴E′BCF′是黄金矩形
(3)由(1)、(2)可发现结论:若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形。
(2)矩形EBCF不是黄金矩形,理由如下:
 |
设AB=a,AD=b(a>b),则BE=BA+AE=a+b,BE′=BA-E′A=a-b,
由ABCD为黄金矩形,得
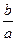 =
=
∴
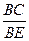 =
=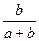 =
=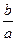 ÷(1+
÷(1+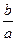 )=
)= ÷(1+
÷(1+ )=
)=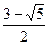 ≠
≠
∴矩形EBCF不是黄金矩形
矩形E′BCF′是黄金矩形
证明:如图4,∵
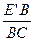 =
=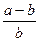 =(1-
=(1-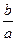 )÷
)÷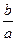 =(1-
=(1- )÷
)÷ =
=
∴E′BCF′是黄金矩形
(3)由(1)、(2)可发现结论:若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形。
略

练习册系列答案
相关题目
 ∽
∽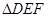 ,
,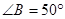 ,
,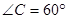 ,则
,则 的度数为 .
的度数为 .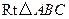 内接于
内接于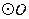 ,
,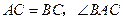 的平分线
的平分线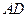 与
与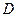 ,与
,与 交于点
交于点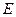 ,延长
,延长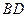 ,与
,与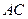 的延长线交于点
的延长线交于点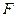 ,连接
,连接 是
是 的中点,连结
的中点,连结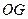 .
.
 ;
;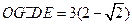 ,求
,求 ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
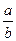 =
=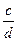 ,判断代数式
,判断代数式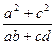 -
-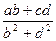 +1值的符号
+1值的符号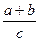 =
=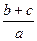 =
=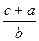 ,求
,求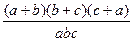 的值。
的值。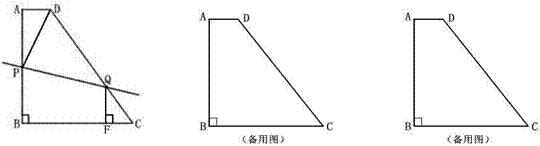
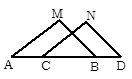
 中,
中, 、
、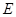 是
是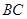 边上的点,
边上的点,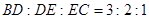 ,
,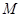 在
在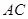
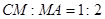 ,
,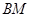 交
交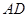 、
、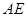 于
于 、
、 ,则
,则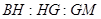 等于 ( )
等于 ( )