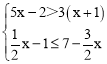题目内容
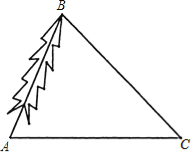
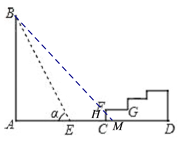
【题目】如图所示,巨型广告牌AB背后有一看台CD,台阶每层高0.3米,且AC=17米,现有一只小狗睡在台阶的FG这,层上晒太阳,设太阳光线与水平地面的夹角为α,当α=60°时,测得广告牌AB在地面上的影长AE=10米,过了一会,当α=45°,问小狗在FG这层是否还能晒到太阳?请说明理由(![]() 取1.73).
取1.73).

【答案】当α=45°时,小狗仍可以晒到太阳.理由见解析
【解析】试题分析:
如下图,假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点M,与FC的交点为点H.在Rt△ABE中由已知条件易得AB≈17.3米,当∠BMA=45°时,易得AM=AB=17.3,由此可得CM=0.3米,则此时CH=CM=0.3米,由台阶每层高为0.3米可知,此时光线刚好照在阶梯的侧面FC的点F处,由此可知小狗此时能够嗮到太阳.
试题解析:
当α=45°时,小狗仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点M,与FC的交点为点H.
当α=60°时,在Rt△ABE中,
∵tan60°=![]() ,
,
∴AB=10tan60°=![]() ≈10×1.73=17.3(米).
≈10×1.73=17.3(米).
∵∠BMA=45°,
∴tan45°=![]() =1,
=1,
此时的影长AM=AB=17.3米,
∴CM=AM﹣AC=17.3﹣17=0.3米,
∴CH=CM=0.3米,
∴大楼的影子落在台阶FC这个侧面上,
∴小狗能晒到太阳.
故答案为:能晒到太阳;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目