题目内容
(2006•旅顺口区)已知抛物线y=x2-4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.(1)求平移后的抛物线解析式;
(2)若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
(3)若将已知的抛物线解析式改为y=ax2+bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移-
 个单位长度,试探索问题(2).
个单位长度,试探索问题(2).
【答案】分析:平移的实质可以可作顶点的平移,先将已知抛物线y=x2-4x+1写成顶点式,再按平移规律写出平移后的函数顶点式.
解答:解:(1)y=x2-4x+1
配方,得y=(x-2)2-3,
向左平移4个单位,得y=(x+2)2-3
∴平移后得抛物线的解析式为y=x2+4x+1;
(2)由(1)知,两抛物线的顶点坐标为(2,-3),(-2,-3)
解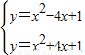 ,
,
得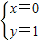
∴两抛物线的交点为(0,1)
由图象知,若直线y=m与两条抛物线有且只有四个交点时,
m>-3且m≠1;
(3)由y=ax2+bx+c配方得y=a(x+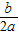 )2+
)2+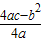 ;
;
向左平移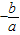 个单位长度得到抛物线的解析式为y=a(x-
个单位长度得到抛物线的解析式为y=a(x-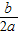 )2+
)2+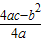 ;
;
∴两抛物线的顶点坐标分别为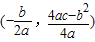 ,
,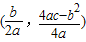
解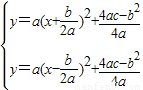
得,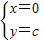
∴两抛物线的交点为(0,c)
由图象知满足(2)中条件的m的取值范围是:
m> 且m≠c.
且m≠c.
点评:此题主要考查抛物线的平移,直线与抛物线的交点等相关知识;此题综合性强,难度较大,要求学生有较好的运算能力.
解答:解:(1)y=x2-4x+1
配方,得y=(x-2)2-3,
向左平移4个单位,得y=(x+2)2-3
∴平移后得抛物线的解析式为y=x2+4x+1;
(2)由(1)知,两抛物线的顶点坐标为(2,-3),(-2,-3)
解
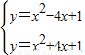 ,
,得
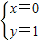
∴两抛物线的交点为(0,1)
由图象知,若直线y=m与两条抛物线有且只有四个交点时,
m>-3且m≠1;
(3)由y=ax2+bx+c配方得y=a(x+
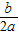 )2+
)2+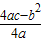 ;
;向左平移
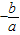 个单位长度得到抛物线的解析式为y=a(x-
个单位长度得到抛物线的解析式为y=a(x-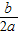 )2+
)2+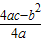 ;
;∴两抛物线的顶点坐标分别为
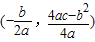 ,
,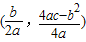
解
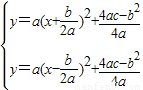
得,
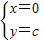
∴两抛物线的交点为(0,c)
由图象知满足(2)中条件的m的取值范围是:
m>
 且m≠c.
且m≠c.点评:此题主要考查抛物线的平移,直线与抛物线的交点等相关知识;此题综合性强,难度较大,要求学生有较好的运算能力.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 个单位长度,试探索问题(2).
个单位长度,试探索问题(2).


