题目内容
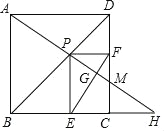
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论_____.(填写序号)
.其中正确结论_____.(填写序号)
【答案】②③
【解析】
①错误;②正确.想办法证明∠GFM+∠AMD=90°即可;③正确,只要证明△CPM∽△HPC,可得![]() ,推出PC2=PMPH,根据对称性可知:PA=PC,可得PA2=PMPH;
,推出PC2=PMPH,根据对称性可知:PA=PC,可得PA2=PMPH;
④错误.利用矩形的性质可知EF=PC,当PC⊥BD时,EF的值最小,最小值为1
解:①错误.因为当点P与BD中点重合时,CM=0,显然FM≠CM;
②正确.连接PC交EF于O.根据对称性可知∠DAP=∠DCP,
∵四边形PECF是矩形,
∴OF=OC,
∴∠OCF=∠OFC,
∴∠OFC=∠DAP,
∵∠DAP+∠AMD=90°,
∴∠GFM+∠AMD=90°,
∴∠FGM=90°,
∴AH⊥EF;
③正确.∵AD∥BH,
∴∠DAP=∠H,
∵∠DAP=∠PCM,
∴∠PCM=∠H,
∵∠CPM=∠HPC,
∴△CPM∽△HPC,
∴![]() ,
,
∴PC2=PMPH,
根据对称性可知:PA=PC,
∴PA2=PMPH.
④错误.∵四边形PECF是矩形,
∴EF=PC,
∴当CP⊥BD时,PC的值最小,此时A、P、C共线,
∵AC=2,
∴PC的最小值为1,
∴EF的最小值为1;
故答案为:②③.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目