题目内容
(1)如图,∠MON=80º,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P. 试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围
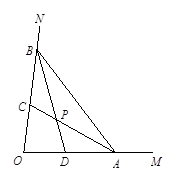
∵在△AOB中,∠MON=80°,∴∠OAB+∠OBA=100° ………… (1分)
又∵AC、BD为角平分线,
∴∠PAB+∠PBA=![]() ∠OAB+
∠OAB+![]() ∠OBA=
∠OBA=![]() ×100°=50° …………… (2分)
×100°=50° …………… (2分)
∴∠APB=180°-(∠PAB+∠PBA)=130°…………………………… (3分)
即随着点A、B位置的变化,∠APB的大小始终不变,为130°.
解析:先根据三角形内角和定理及角平分线的性质求出∠APB的度数,再根据三角形内角和是180°即可求解。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
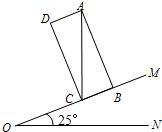 22、如图,∠MON=25°,矩形ABCD的对角线AC⊥ON,边BC在OM上,当AC=3时,AD长是多少?(结果精确到0.01)
22、如图,∠MON=25°,矩形ABCD的对角线AC⊥ON,边BC在OM上,当AC=3时,AD长是多少?(结果精确到0.01)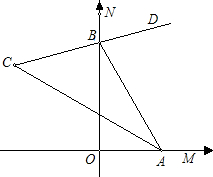 如图,∠MON=90°,点A、B分别在射线OM、ON上移动,BD是∠NBA的平分线,BD的反向延长线与∠BAO的平分线相交于点C.试猜想:∠ACB的大小是否随A、B的移动发生变化?如果保持不变,请给出证明;如果随点A、B的移动发生变化,请给出变化范围.
如图,∠MON=90°,点A、B分别在射线OM、ON上移动,BD是∠NBA的平分线,BD的反向延长线与∠BAO的平分线相交于点C.试猜想:∠ACB的大小是否随A、B的移动发生变化?如果保持不变,请给出证明;如果随点A、B的移动发生变化,请给出变化范围. (2012•济南)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
(2012•济南)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )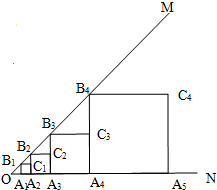 (2013•高要市二模)已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是( )
(2013•高要市二模)已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是( ) 如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,那么满足条件的点P共有( )
如图,∠MON=43°,点A在射线OM上,动点P在射线ON上滑动,要使△AOP为等腰三角形,那么满足条件的点P共有( )