ΧβΡΩΡΎ»ί
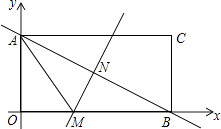
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎRtΓςOAB÷–,ΓœOAB=90Γψ,ΓœBOA=30Γψ,AB=2.»τ“‘OΈΣΉχ±ξ‘≠Βψ,OAΥυ‘Ύ÷±œΏΈΣx÷αΘ§Ϋ®ΝΔ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ,ΒψB‘ΎΒΎ“ΜœσœόΡΎ.ΫΪRtΓςOAB―ΊOB’έΒΰΚσ,ΒψA¬δ‘ΎΒΎ“ΜœσœόΡΎΒΡΒψC¥ΠΘ°
Θ®1Θ©«σΒψCΒΡΉχ±ξΘΜ
Θ®2Θ©»τ≈ΉΈοœΏy=ax2+bxΘ®aΓΌ0Θ©Ψ≠ΙΐCΓΔAΝΫΒψΘ§«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©»τ≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κOBΫΜ”ΎΒψD,ΒψPΈΣœΏΕΈDB…œ“ΜΒψ,ΙΐPΉςy÷αΒΡΤΫ––œΏ,ΫΜ≈ΉΈοœΏ”ΎΒψMΘ°Έ : «Ζώ¥φ‘Ύ’β―υΒΡΒψP, ΙΒΟΥΡ±Ώ–ΈCDPMΈΣΒ»―ϋΧί–ΈΘΩ»τ¥φ‘Ύ,«κ«σ≥ω¥Υ ±ΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®![]() Θ§3Θ©Θ®2Θ©
Θ§3Θ©Θ®2Θ©![]() Θ®3Θ©¥φ‘ΎΘ§Θ®
Θ®3Θ©¥φ‘ΎΘ§Θ® ![]() Θ§
Θ§ ![]() Θ©
Θ©
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©ΙΐCΉςCHΓΆOA”ΎHΘ§
ΓΏ‘ΎRtΓςOAB÷–Θ§ΓœOAB=90ΓψΘ§ΓœBOA=30ΓψΘ§AB=2Θ§ΓύOA=![]() ΓΘ
ΓΘ
ΓΏΫΪRtΓςOAB―ΊOB’έΒΰΚσΘ§ΒψA¬δ‘ΎΒΎ“ΜœσœόΡΎΒΡΒψC¥ΠΘ§
ΓύOC=OA=![]() Θ§ΓœAOC=60ΓψΓΘ
Θ§ΓœAOC=60ΓψΓΘ
ΓύOH=![]() Θ§CH="3" ΓΘ
Θ§CH="3" ΓΘ
ΓύCΒΡΉχ±ξ «Θ®![]() Θ§3Θ©ΓΘ
Θ§3Θ©ΓΘ
Θ®2Θ©ΓΏ≈ΉΈοœΏ![]() Ψ≠ΙΐCΘ®
Ψ≠ΙΐCΘ®![]() Θ§3Θ©ΓΔAΘ®
Θ§3Θ©ΓΔAΘ®![]() Θ§0Θ©ΝΫΒψΘ§
Θ§0Θ©ΝΫΒψΘ§
Γύ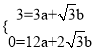 Θ§ΫβΒΟ
Θ§ΫβΒΟ ΓΘΓύ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
ΓΘΓύ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]()
Θ®3Θ©¥φ‘ΎΓΘ
ΓΏ![]() ΒΡΕΞΒψΉχ±ξΈΣΘ®
ΒΡΕΞΒψΉχ±ξΈΣΘ®![]() Θ§3Θ©Θ§Φ¥ΈΣΒψCΓΘ
Θ§3Θ©Θ§Φ¥ΈΣΒψCΓΘ
MPΓΆx÷αΘ§…η¥ΙΉψΈΣNΘ§PNΘΫtΘ§
ΓΏΓœBOAΘΫ300Θ§Υυ“‘ONΘΫ![]()
ΓύPΘ®![]() Θ©
Θ©
ΉςPQΓΆCDΘ§¥ΙΉψΈΣQΘ§MEΓΆCDΘ§¥ΙΉψΈΣEΓΘ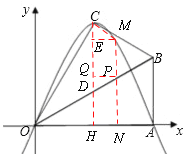
Α―![]() ¥ζ»κ
¥ζ»κ![]() ΒΟΘΚ
ΒΟΘΚ ![]() ΓΘ
ΓΘ
Γύ MΘ®![]() Θ§
Θ§ ![]() Θ©Θ§EΘ®
Θ©Θ§EΘ®![]() Θ§
Θ§ ![]() Θ©ΓΘ
Θ©ΓΘ
Ά§άμΘΚQΘ®![]() Θ§tΘ©Θ§DΘ®
Θ§tΘ©Θ§DΘ®![]() Θ§1Θ©ΓΘ
Θ§1Θ©ΓΘ
“Σ ΙΥΡ±Ώ–ΈCDPMΈΣΒ»―ϋΧί–ΈΘ§÷Μ–ηCEΘΫQDΘ§
Φ¥![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ ![]() Θ§
Θ§ ![]() Θ®…α»ΞΘ©ΓΘ
Θ®…α»ΞΘ©ΓΘ
Γύ PΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§ ![]() Θ©ΓΘ
Θ©ΓΘ
Γύ ¥φ‘Ύ¬ζΉψΧθΦΰΒΡΒψPΘ§ ΙΒΟΥΡ±Ώ–ΈCDPMΈΣΒ»―ϋΧί–ΈΘ§¥Υ ±PΒψΒΡΉχΈΣΘ®![]() Θ§
Θ§ ![]() Θ©ΓΘ
Θ©ΓΘ
Θ®1Θ©ΙΐCΉςCHΓΆOA”ΎHΘ§ΗυΨί’έΒΰΒΟΒΫOC=OA=4Θ§ΓœA0C=60ΓψΘ§«σ≥ωOHΚΆCHΦ¥Ω…ΓΘ
Θ®2Θ©Α―CΘ®![]() Θ§3Θ©ΓΔAΘ®
Θ§3Θ©ΓΔAΘ®![]() Θ§0Θ©¥ζ»κ
Θ§0Θ©¥ζ»κ![]() ΒΟΒΫΖΫ≥ΧΉιΘ§«σ≥ωΖΫ≥ΧΉιΒΡΫβΦ¥Ω…ΓΘ
ΒΟΒΫΖΫ≥ΧΉιΘ§«σ≥ωΖΫ≥ΧΉιΒΡΫβΦ¥Ω…ΓΘ
Θ®3Θ©»γΆΦΘ§ΗυΨίΒ»―ϋΧί–ΈΒΡ≈–Ε®Θ§÷Μ“ΣCEΘΫQDΦ¥Ω…Θ§Ψί¥ΥΝ– Ϋ«σΫβΓΘ