题目内容
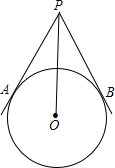 如图,⊙O的半径为2,直线PA、PB为⊙O的切线,A、B为切点,若PA⊥PB,则OP的长为( )
如图,⊙O的半径为2,直线PA、PB为⊙O的切线,A、B为切点,若PA⊥PB,则OP的长为( )A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |
分析:连接OA、OB,则OA⊥AP,OB⊥PB;由HL定理可知Rt△PAO≌Rt△PBO,求出∠APO的度数,根据三角函数值的定义即可求出OP的长.
解答: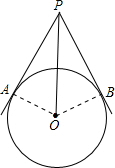 解:连接OA、OB,则OA⊥AP,OB⊥PB,OA=OB=2,
解:连接OA、OB,则OA⊥AP,OB⊥PB,OA=OB=2,
在Rt△PAO与Rt△PBO中,
∵OP=OP,OA=OB,
∴Rt△PAO≌Rt△PBO,
∴∠APO=∠BPO=
∠APB;
∵PA⊥PB,
∴∠APB=90°,
∴∠APO=45°,
在Rt△PAO中,OP=
=
=2
.
故选C.
 解:连接OA、OB,则OA⊥AP,OB⊥PB,OA=OB=2,
解:连接OA、OB,则OA⊥AP,OB⊥PB,OA=OB=2,在Rt△PAO与Rt△PBO中,
∵OP=OP,OA=OB,
∴Rt△PAO≌Rt△PBO,
∴∠APO=∠BPO=
| 1 |
| 2 |
∵PA⊥PB,
∴∠APB=90°,
∴∠APO=45°,
在Rt△PAO中,OP=
| OA |
| sin∠APO |
| 2 | ||||
|
| 2 |
故选C.
点评:此题比较简单,解答此题的关键是连接OA、OB,根据切线的性质解答.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为