题目内容
 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.分析:设道路出入口的边的长度为x米,过点F作FM⊥EH于M,在Rt△EFM中,由勾股定理得出MF的值,就可以求出道路交叉点的正方形的面积,根据正方形的面积为137平方米建立方程,求出其解就可以得出结论.
解答:解:设道路出入口的边的长度为x米,过点F作FM⊥EH于M,
在Rt△EFM中,由勾股定理得:
MF=
x,
∴小正方形的边长为
x米.
∴30x+40x-
x2=137,
3x2-280x+548=0,
(3x-274)(x-2)=0,
解得:x1=
,x2=2.
∵x=
不符合题意,舍去.
答:道路出入口的边的长度为2米.
在Rt△EFM中,由勾股定理得:
MF=
| ||
| 2 |
∴小正方形的边长为
| ||
| 2 |

∴30x+40x-
| 3 |
| 4 |
3x2-280x+548=0,
(3x-274)(x-2)=0,
解得:x1=
| 274 |
| 3 |
∵x=
| 274 |
| 3 |
答:道路出入口的边的长度为2米.
点评:本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,勾股定理的运用,正方形的面积的运用,解答时求出中间小正方形的边长是关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
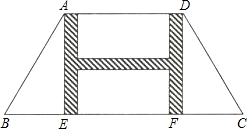 在草坪中修建一条横、纵向的“H”型甬道,甬道宽度相等.甬道面积是整个梯形面积的
在草坪中修建一条横、纵向的“H”型甬道,甬道宽度相等.甬道面积是整个梯形面积的 ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的
”型甬道,甬道宽度相等,甬道面积是整个梯形面积的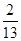 .设甬道的宽为
.设甬道的宽为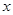 米.
米.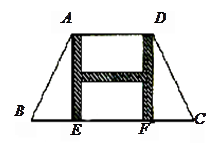
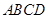 的周长;
的周长;  ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的
”型甬道,甬道宽度相等,甬道面积是整个梯形面积的 .设甬道的宽为
.设甬道的宽为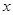 米.
米.
 的周长;
的周长;
 如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
如图,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60°,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.