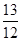题目内容
如果实数a,b,c满足a=2b+ ,且ab+
,且ab+ c2+
c2+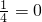 ,那么
,那么 的值是多少?
的值是多少?
解:将a=2b+ 代入ab+
代入ab+ c2+
c2+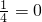 得:
得:
ab+ c2+
c2+ =(2b+
=(2b+ )b+
)b+ c2+
c2+
=[( b)2+2(
b)2+2( b)•
b)• +(
+( )2]+
)2]+ c2
c2
=( b+
b+ )2+
)2+ c2=0,
c2=0,
∴c=0,b=-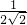 ,
,
∴ =0.
=0.
分析:将a=2b+ 代入ab+
代入ab+ c2+
c2+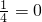 中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,即可得出答案.
中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,即可得出答案.
点评:此题考查了配方法在等式变形中的运用,非负数的性质,关键是通过配方求出c、b的值.
 代入ab+
代入ab+ c2+
c2+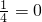 得:
得:ab+
 c2+
c2+ =(2b+
=(2b+ )b+
)b+ c2+
c2+
=[(
 b)2+2(
b)2+2( b)•
b)• +(
+( )2]+
)2]+ c2
c2=(
 b+
b+ )2+
)2+ c2=0,
c2=0,∴c=0,b=-
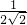 ,
,∴
 =0.
=0.分析:将a=2b+
 代入ab+
代入ab+ c2+
c2+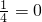 中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,即可得出答案.
中,利用配方法将等式变形为两个非负数的和为0的形式,利用几个非负数的和为0,这几个非负数都为0,即可得出答案.点评:此题考查了配方法在等式变形中的运用,非负数的性质,关键是通过配方求出c、b的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
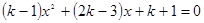 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.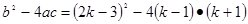
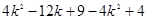
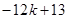 >0
>0