题目内容
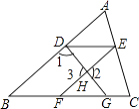
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为 ;
(2)求点![]() 到直线
到直线![]() 的距离;
的距离;
(3)如果点![]() 到直线
到直线![]() 的距离为3,求a的值.
的距离为3,求a的值.
【答案】(1)4 (2)![]() (3)
(3)![]()
【解析】(1)根据勾股定理可得点O(0,0)到⊙P的距离;
(2)过点M作MH⊥l,垂足为点H,通过证明△EOF∽△MHE,由相似三角形的性质可得![]() ,从而得到点M到直线y=2x+1的距离;
,从而得到点M到直线y=2x+1的距离;
(3)两种情况:N在F点的上边;N在F点的下边;进行讨论. 利用相似即可得到a的值.
解:(1)OP=![]() =5,
=5,
点O(0,0)到⊙P的距离为5﹣1=4;
(2)直线![]() 记为
记为![]() ,如图1,过点
,如图1,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
设![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,则
,则![]() .
.
∴![]() .
.
∵![]()
∴![]() ,
,
即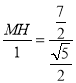 .
.
∴![]() .
.
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
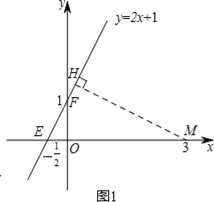
(3)N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
∵△EOF∽△NGF,
∴![]() ,
,
即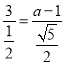 ,
,
∴a=1+3![]() ;
;
N在F点的下边,
同理可得a=1﹣3![]() ;
;
故![]() .
.

练习册系列答案
相关题目