题目内容
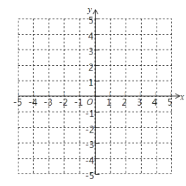
【题目】若函数![]() 的图象与
的图象与![]() 轴恰好有三个公共点,则实数
轴恰好有三个公共点,则实数![]() 的值是 ( )
的值是 ( )
A. ![]() B.
B. ![]() C. 1D. 2
C. 1D. 2
【答案】D
【解析】
把m=-2、-1、1、2分别代入函数解析式,分类讨论:当x≥0或x<0时得到二次函数解析式,然后根据抛物线与x轴的交点问题确定图象与x轴的公共点的个数.
解:A、当m=-2时,y=x2-2|x|+4,当x≥0时,抛物线y=x2-2x+4与x轴没有公共点;当x<0时,抛物线y=x2+2x+4 x轴没有公共点,所以A选项错误;
B、当m=-1时,y= x2-2|x|+3,当x≥0时,抛物线y=x2-2x+3与x轴没有公共点;当x<0时,抛物线y=x2+2x+3与轴没有公共点,所以B选项错误;
C、当m=1时,y=x2-2|x|+1,当x≥0时,抛物线y=x2-2x+1与x轴有1个公共点;当x<0时,抛物线y=x2+2x+1与x轴有1个公共点,所以C选项错误;
D、m=2是,y=x2-2|x|,抛物线y=x2-2x与x轴的交点坐标为(0,0)、(2,0);当x<0时,抛物线y=x2+2x与x轴的交点坐标为(-2,0),所以D选项正确.
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目