题目内容
（1998•黄冈）如图，⊙O是△ABC的外接圆，AD是BC边上的高，已知BD=8，CD=3，AD=6，则直径AM的长为 ．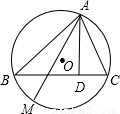
【答案】分析：如图，连接BM．利用勾股定理得AB=10，AC=3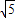
；由AM是直径，可得∠ABM=90°．所以sinC=sinM=AD：AC=AB：AM，根据这个比例式可以求出AM．
解答：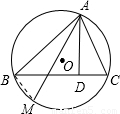
解：连接BM．
∵AD是BC边上的高，
∴△ABD，△ADC都是直角三角形，
由勾股定理得，AB=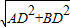
=
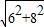=10，
AC=
=
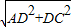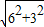=3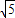
；
又∵AM是直径，则∠ABM=90°，
由圆周角定理知，∠C=∠M，
∴sinC=sinM，即AD：AC=AB：AM，6：3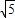
=10：AM，
解得AM=5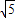
．
点评：本题利用了直径所对的圆周角是直角，圆周角定理，直角三角形的性质，正弦的概念，勾股定理等来求解，综合性较强．
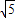；由AM是直径，可得∠ABM=90°．所以sinC=sinM=AD：AC=AB：AM，根据这个比例式可以求出AM．解答：
解：连接BM．∵AD是BC边上的高，
∴△ABD，△ADC都是直角三角形，
由勾股定理得，AB=
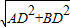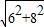==10，AC=
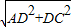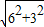==3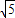；又∵AM是直径，则∠ABM=90°，
由圆周角定理知，∠C=∠M，
∴sinC=sinM，即AD：AC=AB：AM，6：3
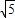=10：AM，解得AM=5
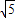．点评：本题利用了直径所对的圆周角是直角，圆周角定理，直角三角形的性质，正弦的概念，勾股定理等来求解，综合性较强．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
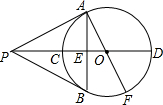（1998•黄冈）如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，下列结论：①∠ABP=∠AOP；②
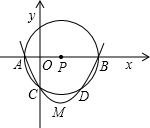（1998•黄冈）如图，直角坐标系中，O为坐标原点，A点坐标为（-3，0），B点坐标为（12，0），以AB为直径作⊙P与y轴的负半轴交于点C．抛物线y=ax2+bx+c经过A、B、C三点，其顶点为M点．
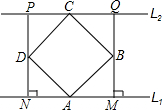（1998•黄冈）如图，已知四边形ABCD是正方形，分别过A、C两点作l1∥l2，作BM⊥l1于M，DN⊥l1于N，直线MB、ND分别交l2于Q、P．求证：四边形PQMN是正方形．
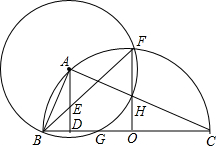（1998•黄冈）如图，⊙O是△ABC的外接圆，BC是直径，以顶点A为圆心，AB长为半径的圆交⊙O于F点，交BC于G点（AB＜OB）．AD⊥BC于D，AD与BF交于E点，OF交⊙A于H点．求证：