题目内容
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |
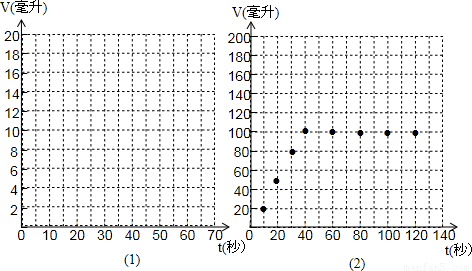
(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水______千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?
【答案】分析:实验一:
(1)根据图中的数据直接在坐标系中描出各点即可;
(2)先设出V与t的函数关系式为V=kt+b,根据表中数据,得出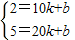 ,求出V与t的函数关系式,再根据
,求出V与t的函数关系式,再根据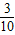 t-1≥100和量筒的容量,即可求出多少秒后,量筒中的水会满面开始溢出;
t-1≥100和量筒的容量,即可求出多少秒后,量筒中的水会满面开始溢出;
(3)根据(2)中的函数关系式,把t=60代入即可求出答案.
实验二:
根据小李同学接水的量筒装满后开始溢出,量筒内的水不再发生变化,即可得出图象中会出现与横轴“平行”的部分.
解答:解:实验一:
(1)画图象如图所示:
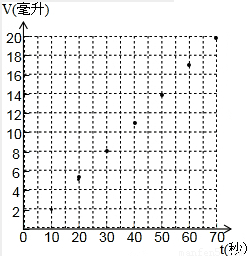
(2)设V与t的函数关系式为V=kt+b,
根据表中数据知:
当t=10时,V=2;
当t=20时,V=5,
所以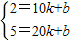 ,
,
解得: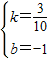 ,
,
所以V与t的函数关系式为V=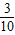 t-1,
t-1,
由题意得: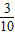 t-1≥100,
t-1≥100,
解得t≥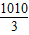 =336
=336 ,
,
所以337秒后,量筒中的水会满面开始溢出;
(3)一小时会漏水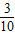 ×3600-1=1079(毫升)=1079(克)≈1.1千克;
×3600-1=1079(毫升)=1079(克)≈1.1千克;
故答案为:1.1;
实验二:
因为小李同学接水的量筒装满后开始溢出,量筒内的水位不再发生变化,
所以图象中会出现与横轴“平行”的部分.
点评:此题考查了一次函数的应用,解题的关键是根据已知条件求出V与t的函数关系式,在解题时要能把函数的图象与实际相结合.
(1)根据图中的数据直接在坐标系中描出各点即可;
(2)先设出V与t的函数关系式为V=kt+b,根据表中数据,得出
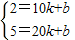 ,求出V与t的函数关系式,再根据
,求出V与t的函数关系式,再根据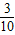 t-1≥100和量筒的容量,即可求出多少秒后,量筒中的水会满面开始溢出;
t-1≥100和量筒的容量,即可求出多少秒后,量筒中的水会满面开始溢出;(3)根据(2)中的函数关系式,把t=60代入即可求出答案.
实验二:
根据小李同学接水的量筒装满后开始溢出,量筒内的水不再发生变化,即可得出图象中会出现与横轴“平行”的部分.
解答:解:实验一:
(1)画图象如图所示:

(2)设V与t的函数关系式为V=kt+b,
根据表中数据知:
当t=10时,V=2;
当t=20时,V=5,
所以
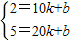 ,
,解得:
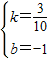 ,
,所以V与t的函数关系式为V=
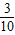 t-1,
t-1,由题意得:
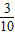 t-1≥100,
t-1≥100,解得t≥
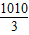 =336
=336 ,
,所以337秒后,量筒中的水会满面开始溢出;
(3)一小时会漏水
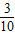 ×3600-1=1079(毫升)=1079(克)≈1.1千克;
×3600-1=1079(毫升)=1079(克)≈1.1千克;故答案为:1.1;
实验二:
因为小李同学接水的量筒装满后开始溢出,量筒内的水位不再发生变化,
所以图象中会出现与横轴“平行”的部分.
点评:此题考查了一次函数的应用,解题的关键是根据已知条件求出V与t的函数关系式,在解题时要能把函数的图象与实际相结合.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |
(1)在图1的坐标系中描出上表中数据对应的点;
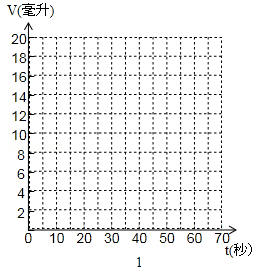
(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克)
实验二:
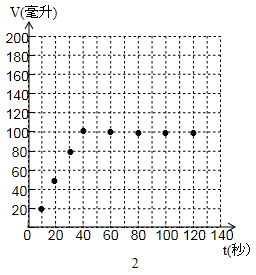
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
|
时间t(秒) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
漏出的水量V(毫升) |
2 |
5 |
8 |
11 |
14 |
17 |
20 |
(1)在图1的坐标系中描出上表中数据对应的点;
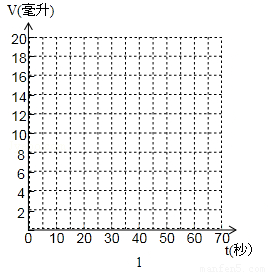
(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?
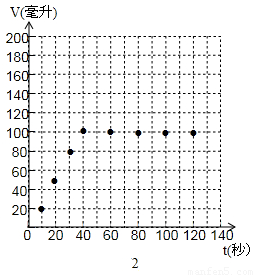
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
(1)在图1的坐标系中描出上表中数据对应的点;
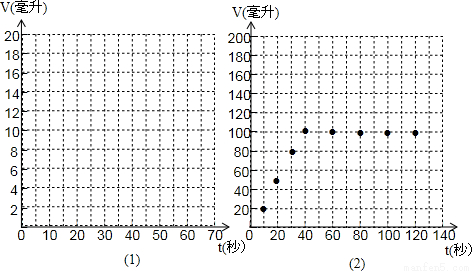
(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水______千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |

(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水______千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?
