题目内容
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.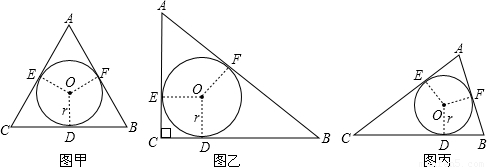
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
【答案】分析:(1)首先运用刻度尺进行准确测量,然后根据周长等于三边之和进行计算,根据面积等于分割成的三个三角形的面积进行计算;
(2)根据表格中的数据,易猜想得到r= .再根据三角形的总面积等于分割成的三部分的面积进行计算证明.
.再根据三角形的总面积等于分割成的三部分的面积进行计算证明.
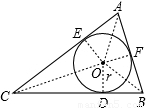
解答:解:(1)
(2)由图表信息猜测,得r= (或者2s=Lr)并且此关系对一般三角形都成立.
(或者2s=Lr)并且此关系对一般三角形都成立.
证明:在任意△ABC中,⊙O是△ABC的内切圆,连接OA、OB、OD,得
S= BC•r+
BC•r+ AC•r+
AC•r+ AB•r=
AB•r= Lr
Lr
∴r=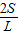 .
.
点评:此题导出了三角形的内切圆半径的一个公式,即三角形的内切圆的半径等于面积的2倍除以周长.
(2)根据表格中的数据,易猜想得到r=
 .再根据三角形的总面积等于分割成的三部分的面积进行计算证明.
.再根据三角形的总面积等于分割成的三部分的面积进行计算证明.解答:解:(1)
| AC | BC | AB | r | L | s | |
| 图甲 | 2.0 | 2.0 | 2.0 | 0.6 | 6.0 | 1.7(或1.8) |
| 图乙 | 3.0 | 4.0 | 5.0 | 1.0 | 12.0 | 6.0 |

(2)由图表信息猜测,得r=
 (或者2s=Lr)并且此关系对一般三角形都成立.
(或者2s=Lr)并且此关系对一般三角形都成立.证明:在任意△ABC中,⊙O是△ABC的内切圆,连接OA、OB、OD,得
S=
 BC•r+
BC•r+ AC•r+
AC•r+ AB•r=
AB•r= Lr
Lr∴r=
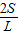 .
.点评:此题导出了三角形的内切圆半径的一个公式,即三角形的内切圆的半径等于面积的2倍除以周长.

练习册系列答案
相关题目
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.
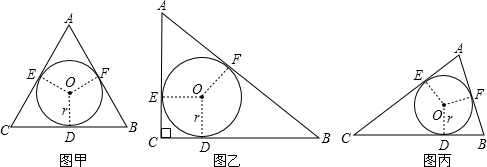
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与L、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?

(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.

(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.
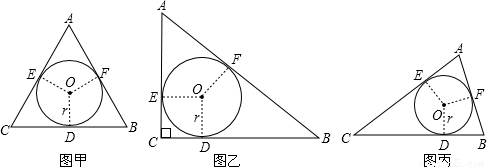
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与L、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?

(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.
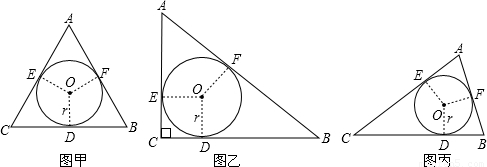
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与L、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?

(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |