题目内容
(2002•潍坊)如图,点M、N分别是?ABCD的DC、CB边的中点,连接AM、AN,分别交□ABCD的对角线BD于E、F点,(1)求证:点E、F是线段BD的三等分点;
(2)若?ABCD的面积为S,求△AMN的面积.
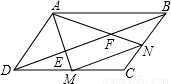
【答案】分析:(1)根据平行四边形的性质,先证明△DEM∽△BEA,△BNF∽△DFA,再根据相似三角形的性质得出点E、F是线段BD的三等分点;
(2)根据S△AMN=S四边形ABCD-S△AMD-S△NMC+S△ABN可求.
解答:(1)证明:∵四边形ABCD为平行四边形和△DEM∽△BEA
又∵M为DC的中点,所以DM:AB=1:2,∴DE:BE=1:2
即E是DB的三等分点
同理△BNF∽△DFA
由N为BC的中点,得F是DB的三等分点.
所以E,F为线段BD的三等分点.
(2)解:因为M.N是DC和CB的中点,
在△ABC中,S△AMD=S△ABN=S四边形ABCD=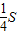 ,
,
S△NMC= S△BCD=
S△BCD= S四边形ABCD=
S四边形ABCD= S
S
所以S△AMN=S四边形ABCD-S△AMD-S△NMC+S△ABN=S-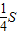 -
-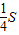 -
- S=
S=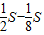 =
=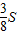 .
.
点评:本题考查了平行四边形的性质,相似三角形的判定和性质.要熟悉相似三角形的性质:相似三角形的面积比是相似比的平方.
(2)根据S△AMN=S四边形ABCD-S△AMD-S△NMC+S△ABN可求.
解答:(1)证明:∵四边形ABCD为平行四边形和△DEM∽△BEA
又∵M为DC的中点,所以DM:AB=1:2,∴DE:BE=1:2
即E是DB的三等分点
同理△BNF∽△DFA
由N为BC的中点,得F是DB的三等分点.
所以E,F为线段BD的三等分点.
(2)解:因为M.N是DC和CB的中点,
在△ABC中,S△AMD=S△ABN=S四边形ABCD=
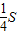 ,
,S△NMC=
 S△BCD=
S△BCD= S四边形ABCD=
S四边形ABCD= S
S所以S△AMN=S四边形ABCD-S△AMD-S△NMC+S△ABN=S-
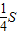 -
-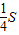 -
- S=
S=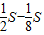 =
=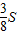 .
.点评:本题考查了平行四边形的性质,相似三角形的判定和性质.要熟悉相似三角形的性质:相似三角形的面积比是相似比的平方.

练习册系列答案
相关题目