题目内容
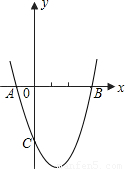
 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.(1)试确定b、c的值;
(2)过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点,试确定△MCD的形状.
分析:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得到关于b、c的二元一次方程组,解即可;
(2)由于CD∥x轴,而且抛物线关于对称轴对称,于是易知l也是CD的垂直平分线,进而可得MC=MD,从而可证.
(2)由于CD∥x轴,而且抛物线关于对称轴对称,于是易知l也是CD的垂直平分线,进而可得MC=MD,从而可证.
解答: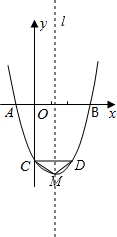 解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
,
解得
,
故b=-2,c=-3;
(2)∵CD∥x轴,抛物线关于对称轴l对称,
∴l⊥x轴,
∴l是CD的垂直平分线,
∴MC=MD,
∵抛物线的解析式为:y=x2-2x-3=(x-1)2-4,
∴点M的坐标为:(1,-4),点C的坐标为:(0,-3),
∴点D的坐标为:(2,-3),
∴CD=2,CM=DM=
,
∴CM2+DM2=CD2,
∴△MCD是等腰直角三角形.
 解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
解:(1)把(-1,0)、(3,0)代入y=x2+bx+c中,得
|
解得
|
故b=-2,c=-3;
(2)∵CD∥x轴,抛物线关于对称轴l对称,
∴l⊥x轴,
∴l是CD的垂直平分线,
∴MC=MD,
∵抛物线的解析式为:y=x2-2x-3=(x-1)2-4,
∴点M的坐标为:(1,-4),点C的坐标为:(0,-3),
∴点D的坐标为:(2,-3),
∴CD=2,CM=DM=
| 2 |
∴CM2+DM2=CD2,
∴△MCD是等腰直角三角形.
点评:本题考查了待定系数法求函数解析式、二次函数的性质,解题的关键是注意二次函数具有对称性.

练习册系列答案
相关题目
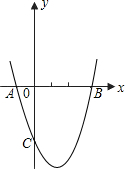 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.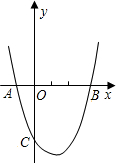 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点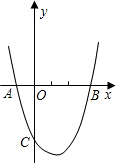 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点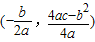 .
.