题目内容
【题目】如图,已知ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.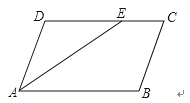
(1)作∠BCD的角平分线CF(尺规作图,保留痕迹,不写作法)
(2)求证:AE=CF
【答案】
(1)
解:如图;①以B为圆心,以任意长为半径化弧,分别与AB,BC的交于点M,N,
②分别以M,N为圆心,大于![]() MN为半径画弧,两弧交于点P,
MN为半径画弧,两弧交于点P,
③作射线BP,交CD于点F,则BF即为所求
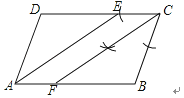
(2)
∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠DAB=∠DCB,
又∵AE平分∠BAD,CF平分∠BCD,
∴∠DAE=![]() ∠DAB,∠BCF=
∠DAB,∠BCF=![]() ∠DCB,
∠DCB,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
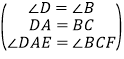 ,
,
∴△DAE≌△BCF(ASA),
∴AE=CF.
【解析】(1)首先以B为圆心,以任意长为半径化弧,分别与AB,BC的交于点M,N,再分别以M,N为圆心,大于![]() MN为半径画弧,两弧交于点P,作射线BP,交CD于点F,则BF即为所求;
MN为半径画弧,两弧交于点P,作射线BP,交CD于点F,则BF即为所求;
(2)由ABCD中,AE平分∠BAD,CF平分∠BCD,易得AD=BC,∠D=∠B,∠DAB=∠DCB,∠DAE=∠BCF,继而证得△DAE≌△BCF,则可证得结论.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目