Question

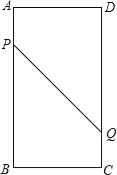
【题目】如图，在正方形中，以为边作等边，延长，分别交于点，连接、、与相交于点，给出下列结论：①；②；③；④，其中正确的是__________．

Answer 1

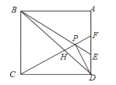
【答案】①②③④

【解析】

①正确．利用直角三角形30度角的性质即可解决问题；②正确，通过计算证明∠BPD=135°，即可判断； ③正确，根据两角相等两个三角形相似即可判断；④正确．利用相似三角形的性质即可证明．

∵△BPC是等边三角形，
∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，
在正方形ABCD中，
∵AB=BC=CD，∠A=∠ABC =∠ADC=∠BCD=90°，
∴∠ABE=∠DCF=90°-60°=30°，

在和中，

，

∴，

∴，

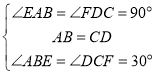∴在中，∠A=90°，∠ABE=30°，

∴，故①正确；

∵PC=CD，∠PCD=30°，
∴∠PDC=∠DPC=75°，

∴∠BPD=∠BPC+∠DPC =60°+75°=135°，故②正确；

∵∠ADC =90°，∠PDC=75°，
∴∠EDP=∠ADC -∠PDC =90°-75°=15°，
∵∠DBA=45°，∠ABE=30°，
∴∠EBD=∠DBA -∠ABE =45°-30°=15°，
∴∠EDP=∠EBD=15°，
∵∠DEP=∠BED，
∴△PDE∽△DBE，故③正确；

∵△PDE∽△DBE，

∴，

∴，故④正确；

综上，①②③④都正确，

故答案为：①②③④．