题目内容
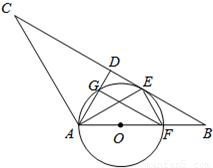
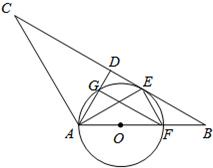 (2010•德州)如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点,交AD于点G,交AB于点F.
(2010•德州)如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点,交AD于点G,交AB于点F.(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,则∠EFG=
30
30
度.分析:(1)连接OE,证OE⊥BC即可.因为AD⊥BC,所以转证OE∥AD.由AE平分∠BAD,OA=OE易得此结论.
(2)∠EFG=∠GAE=∠EAO=∠AEO.根据已知条件易得∠B=30°,∠EOB=60°.从而求解.
(2)∠EFG=∠GAE=∠EAO=∠AEO.根据已知条件易得∠B=30°,∠EOB=60°.从而求解.
解答:证明: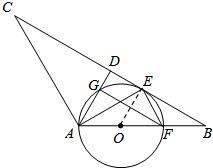 (1)连接OE. (1分)
(1)连接OE. (1分)
∵AB=AC且D是BC中点,
∴AD⊥BC.
∵AE平分∠BAD,
∴∠BAE=∠DAE. (2分)
∵OA=OE,
∴∠OAE=∠OEA.
∴∠OEA=∠DAE.
∴OE∥AD.
∴OE⊥BC.
∴BC是⊙O的切线. (3分)
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°. (1分)
∴∠EOB=60°. (1分)
∴∠EAO=∠EAG=30°. (1分)
∴∠EFG=30°. (1分)
 (1)连接OE. (1分)
(1)连接OE. (1分)∵AB=AC且D是BC中点,
∴AD⊥BC.
∵AE平分∠BAD,
∴∠BAE=∠DAE. (2分)
∵OA=OE,
∴∠OAE=∠OEA.
∴∠OEA=∠DAE.
∴OE∥AD.
∴OE⊥BC.
∴BC是⊙O的切线. (3分)
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°. (1分)
∴∠EOB=60°. (1分)
∴∠EAO=∠EAG=30°. (1分)
∴∠EFG=30°. (1分)
点评:此题考查了切线的判定、等腰三角形性质等知识点,难度中等.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目