题目内容
 如图,在直角坐标平面内,O为原点,已知抛物线y=x2+bx+3经过点A(3,0),与y轴的交点为B,设此抛物线的顶点为C.
如图,在直角坐标平面内,O为原点,已知抛物线y=x2+bx+3经过点A(3,0),与y轴的交点为B,设此抛物线的顶点为C.(1)求b的值和C的坐标;
(2)若点C1与C关于x轴对称,求证:点C1在直线AB上;
(3)在(2)的条件下,在抛物线y=x2+bx+3的对称轴上是否存在一点D,使四边形OC1DB是等腰梯形?若存在,请求出点D的坐标;若不存在,请简要说明理由.
分析:(1)由抛物线y=x2+bx+3经过点A(3,0),利用待定系数法即可求得b的值,然后求得此抛物线的解析式,配方,即可求得顶点为C的坐标;
(2)由点C1与C关于x轴对称,即可求得点C1的坐标,又由待定系数法求得直线AB的解析式,即可证得点C1在直线AB上;
(3)分为若BD∥OC1与DC1∥OB去分析,根据平行线的性质与等腰三角形的性质,即可求得点D的坐标.
(2)由点C1与C关于x轴对称,即可求得点C1的坐标,又由待定系数法求得直线AB的解析式,即可证得点C1在直线AB上;
(3)分为若BD∥OC1与DC1∥OB去分析,根据平行线的性质与等腰三角形的性质,即可求得点D的坐标.
解答:解:(1)∵抛物线y=x2+bx+3经过点A(3,0),
∴9+3b+3=0,
解得:b=-4,
∴此抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
∴此抛物线的顶点为C的坐标为(2,-1);
(2)∵点C1与C关于x轴对称,
∴点C1的坐标为(2,1),
∵当x=0时,y=3,
∴点B的坐标为(0,3),
设直线AB的解析式为:y=kx+b,
∴
,
解得:
,
∴直线AB的解析式为:y=-x+3,
∵-2+3=1,
∴点C1在直线AB上;
(3)存在.
如图1,若BD∥OC1,
∵直线OC1的解析式为:y=
x,
∴设直线BD的解析式为:y=
x+b,
则b=3,
∴直线BD的解析式为:y=
x+3,
设点D(a,
a+3),
∵AB=C1D,
∴(a-2)2+(
a+3-1)2=9,
∴a=-
(不合题意,舍去)或a=2(此题是平行四边形,舍去);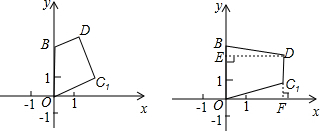
如图2,当DC1∥OB,
过点D作DE⊥OB于E,过点C作FC⊥x轴于F,
∵四边形OC1DB是等腰梯形,
∴BE=CF=1,DE=OF=2,
∴CD=OB-2BE=3-2=1,
∴DF=2,
∴点D的坐标为(2,2).
故带D的坐标为(2,2).
∴9+3b+3=0,
解得:b=-4,
∴此抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
∴此抛物线的顶点为C的坐标为(2,-1);
(2)∵点C1与C关于x轴对称,
∴点C1的坐标为(2,1),
∵当x=0时,y=3,
∴点B的坐标为(0,3),
设直线AB的解析式为:y=kx+b,
∴
|
解得:
|
∴直线AB的解析式为:y=-x+3,
∵-2+3=1,
∴点C1在直线AB上;
(3)存在.
如图1,若BD∥OC1,
∵直线OC1的解析式为:y=
| 1 |
| 2 |
∴设直线BD的解析式为:y=
| 1 |
| 2 |
则b=3,
∴直线BD的解析式为:y=
| 1 |
| 2 |
设点D(a,
| 1 |
| 2 |
∵AB=C1D,
∴(a-2)2+(
| 1 |
| 2 |
∴a=-
| 2 |
| 5 |
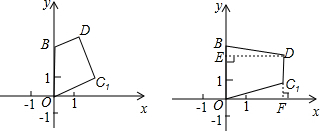
如图2,当DC1∥OB,
过点D作DE⊥OB于E,过点C作FC⊥x轴于F,
∵四边形OC1DB是等腰梯形,
∴BE=CF=1,DE=OF=2,
∴CD=OB-2BE=3-2=1,
∴DF=2,
∴点D的坐标为(2,2).
故带D的坐标为(2,2).
点评:此题考查了待定系数法求函数的解析式,等腰梯形的性质,平行线的性质以及点与函数的关系.此题综合性很强,难度较大,解题的关键是方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
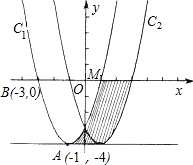 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)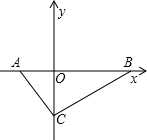 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=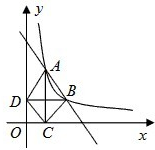 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是